题目内容
已知椭圆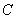 :
: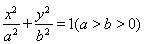 的离心率为
的离心率为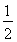 ,右焦点
,右焦点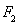 到直线
到直线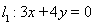 的距离为
的距离为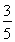 .
.
(1)求椭圆 的方程;
的方程;
(2)过椭圆右焦点F2斜率为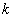 (
(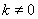 )的直线
)的直线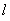 与椭圆
与椭圆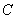 相交于
相交于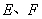 两点,
两点,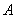 为椭圆的右顶点,直线
为椭圆的右顶点,直线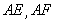 分别交直线
分别交直线 于点
于点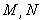 ,线段
,线段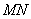 的中点为
的中点为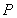 ,记直线
,记直线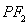 的斜率为
的斜率为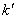 ,求证:
,求证: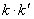 为定值.
为定值.
【答案】
(1)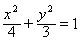 .(2)证明见解析.
.(2)证明见解析.
【解析】
试题分析:(1)利用椭圆的几何性质,建立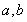 的方程组即得;
的方程组即得;
(2)要证明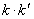 为定值,须从确定两直线斜率的表达式入手.根据题目的条件,应注意设出
为定值,须从确定两直线斜率的表达式入手.根据题目的条件,应注意设出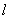 的直线方程,并与椭圆方程联立,应用韦达定理,建立
的直线方程,并与椭圆方程联立,应用韦达定理,建立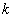 与坐标的联系;确定
与坐标的联系;确定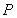 的坐标,将斜率
的坐标,将斜率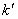 用坐标表示.得到
用坐标表示.得到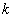 ,
,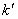 的关系即得证.
的关系即得证.
设过点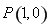 的直线
的直线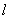 方程为:
方程为: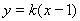 ,
,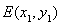 ,点
,点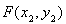 ,
,
将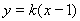 代入椭圆
代入椭圆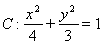 整理得:
整理得: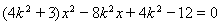
应用韦达定理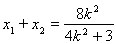
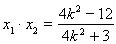 ;
;
根据直线 的方程为:
的方程为: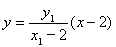 ,直线
,直线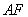 的方程为:
的方程为: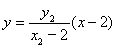
令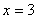 ,得点
,得点 ,
, ,点
,点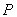
 ;
;
由直线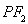 的斜率为
的斜率为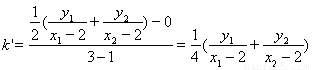
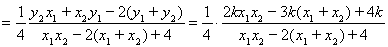 ,
,
将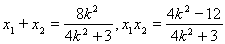 代入上式得到
代入上式得到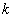 ,
, 的关系即得证.
的关系即得证.
试题解析:(1)由题意得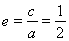 ,
,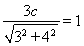 , 2分
, 2分
所以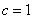 ,
,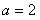 ,所求椭圆方程为
,所求椭圆方程为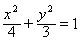 . 4分
. 4分
(2)设过点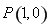 的直线
的直线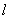 方程为:
方程为: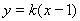 ,
,
设点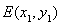 ,点
,点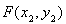 5分
5分
将直线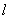 方程
方程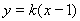 代入椭圆
代入椭圆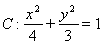
整理得: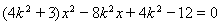 6分
6分
因为点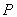 在椭圆内,所以直线
在椭圆内,所以直线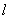 和椭圆都相交,
和椭圆都相交,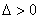 恒成立,
恒成立,
且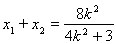
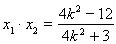 7分
7分
直线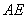 的方程为:
的方程为: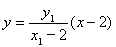 ,直线
,直线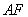 的方程为:
的方程为: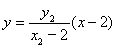
令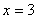 ,得点
,得点 ,
, ,
,
所以点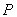 的坐标
的坐标 9分
9分
直线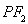 的斜率为
的斜率为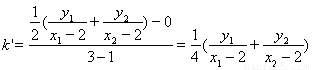
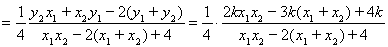 11分
11分
将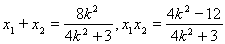 代入上式得:
代入上式得:
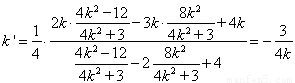
所以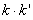 为定值
为定值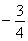 13分
13分
考点:椭圆的几何性质,直线与圆锥曲线的位置关系,韦达定理,直线的斜率与方程.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 已知椭圆E的离心率为e,两焦点为F1,F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个公共点,若
已知椭圆E的离心率为e,两焦点为F1,F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个公共点,若 如图,在平面直角坐标系xOy中,椭圆C:
如图,在平面直角坐标系xOy中,椭圆C: