题目内容
已知抛物线y=-x2+2过其上一点P引抛物线的切线l,l与坐标轴在第一象限围成△AOB,求△AOB面积S的最小值,并求此时切线l的方程.
【答案】分析:设切点P(x,-x2+2)(x>0),由y=-x2+2得y'=-2x,知kl=-2x,故l的方程为:y-(-x2+2)=-2x(x-x).令y=0,得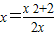 ,令x=0,得y=x2+2,三角形的面积为
,令x=0,得y=x2+2,三角形的面积为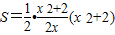 ,由此能求出l的方程.
,由此能求出l的方程.
解答:解:设切点P(x,-x2+2)(x>0)
由y=-x2+2得y'=-2x,
∴kl=-2x,
∴l的方程为:y-(-x2+2)=-2x(x-x)…(3分)
令y=0,得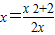 ,令x=0,得y=x2+2,
,令x=0,得y=x2+2,
三角形的面积为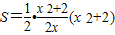 ,x>0…(6分)
,x>0…(6分)
令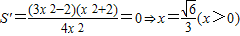 …(8分)
…(8分)
当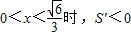 ;
;
当
∴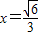 时,
时,
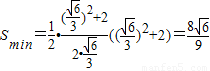 ,…(10分)
,…(10分)
此时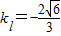 ,
,
切点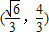 ,
,
故l的方程为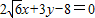 .…(12分)
.…(12分)
点评:本题考查直线与圆锥曲线的综合应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
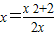 ,令x=0,得y=x2+2,三角形的面积为
,令x=0,得y=x2+2,三角形的面积为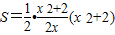 ,由此能求出l的方程.
,由此能求出l的方程.解答:解:设切点P(x,-x2+2)(x>0)
由y=-x2+2得y'=-2x,
∴kl=-2x,
∴l的方程为:y-(-x2+2)=-2x(x-x)…(3分)
令y=0,得
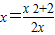 ,令x=0,得y=x2+2,
,令x=0,得y=x2+2,三角形的面积为
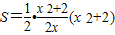 ,x>0…(6分)
,x>0…(6分)令
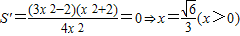 …(8分)
…(8分)当
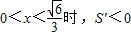 ;
; 当

∴
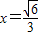 时,
时,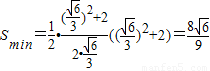 ,…(10分)
,…(10分)此时
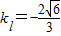 ,
,切点
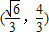 ,
,故l的方程为
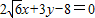 .…(12分)
.…(12分)点评:本题考查直线与圆锥曲线的综合应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
已知抛物线y=-x2+3上存在关于直线x+y=0对称的相异两点A、B,则|AB|等于( )
| A、3 | ||
| B、4 | ||
C、3
| ||
D、4
|
已知抛物线y=x2上有一定点A(-1,1)和两动点P、Q,当PA⊥PQ时,点Q的横坐标取值范围是( )
| A、(-∞,-3] | B、[1,+∞) | C、[-3,1] | D、(-∞,-3]∪[1,+∞) |