题目内容
在数列 中,若
中,若 ,
, ,则
,则 .
.
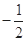 .
.
解析试题分析:由 变形为
变形为 ,即有
,即有 ,令
,令 ,则有
,则有 ,说明
,说明 与
与 互为倒数关系,而由
互为倒数关系,而由 有
有 ,则
,则 ,同理
,同理 ……,因此有
……,因此有 ,所以
,所以 ,故
,故
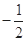 .
.
考点:运用数列特殊递推关系解决问题,本题要注意构造新数列进行归纳寻求相应规律,从而解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第 行有
行有 个数且两端的数均为
个数且两端的数均为
 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如 ,
, ,
, , ,则第10行第4个数(从左往右数)为( )
, ,则第10行第4个数(从左往右数)为( )
A. | B. |
C. | D. |
数列 的前项和为
的前项和为 ,则
,则 的值依次为( )
的值依次为( )
| A.3,4 | B.2,8 | C.3,18 | D.3,14 |
 中,
中, ,则数列
,则数列 =______________.
=______________. ,且对任意
,且对任意 都有
都有 ;②
;② 。则
。则 的值为____________。
的值为____________。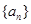 满足
满足 ,则
,则 .
. 中,
中, (
( ),那么此数列
),那么此数列 满足
满足 ,则该数列的通项公式
,则该数列的通项公式 _________.
_________.