题目内容
(本小题满分12分) 已知命题
 表示焦点在
表示焦点在 轴的双曲线,命题
轴的双曲线,命题
 是增函数,若
是增函数,若 或
或 为真命题,
为真命题, 且
且 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
 或
或 .
.
【解析】
试题分析:先分别确定 为真时
为真时 的取值范围,进行根据
的取值范围,进行根据 或
或 为真命题,
为真命题, 且
且 为假命题,作出判断
为假命题,作出判断 一真一假,最后分两
一真一假,最后分两 真
真 假与
假与 假
假 真两种情况求取参数
真两种情况求取参数 的取值范围,并将这种情况的取值范围取并集即可解决.
的取值范围,并将这种情况的取值范围取并集即可解决.
试题解析:由 表示焦点在
表示焦点在 轴的双曲线得
轴的双曲线得
即 得
得
 是增函数,须
是增函数,须 即
即
由于 或
或 为真命题,
为真命题, 且
且 为假命题 故
为假命题 故 中一个真,另一个为假命题
中一个真,另一个为假命题
若 真
真 假,此时
假,此时 的解集为空集
的解集为空集
若 假
假 真,则
真,则 或
或
因此, 或
或 .
.
考点:1.双曲线的标准方程;2.指数函数的图象与性质;3.简单的逻辑用语;4.分类讨论的思想.
考点分析: 考点1:双曲线的标准方程 考点2:双曲线的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
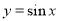 B、
B、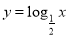 C、
C、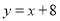 D、
D、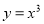
 ,则这四个数的大小关系是( )
,则这四个数的大小关系是( ) B.
B. C.
C. D.
D.
 与
与 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
 ”是“
”是“ ”的( )
”的( ) 有两个零点,则
有两个零点,则 应满足的充要条件是 .
应满足的充要条件是 . , 则命题甲:
, 则命题甲: 是
是 与
与 的等差中项,命题乙:动点
的等差中项,命题乙:动点 的轨迹是椭圆,则甲是乙的 ( ).
的轨迹是椭圆,则甲是乙的 ( ). ,其中
,其中 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ,
, ,
, ,若直线
,若直线
 与函数
与函数 的图象恰有两个不同的交点,则
的图象恰有两个不同的交点,则 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. D.
D.
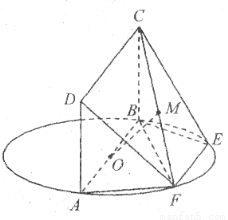
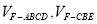 ,求
,求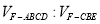 .
.