题目内容
如图,已知直线l与抛物线 相切于点P(2,1),且与
相切于点P(2,1),且与 轴交于点A,定点B的坐标为(2,0) .
轴交于点A,定点B的坐标为(2,0) .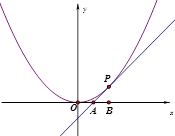
(1)若动点M满足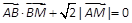 ,求点M的轨迹C;
,求点M的轨迹C;
(2)若过点B的直线l(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
(1)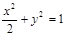 (2)(
(2)(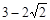 ,1)
,1)
解析试题分析:(1)先对原函数求导,然后求出斜率,再利用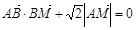 进行整理即可.
进行整理即可.
(2)先设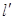 方程为
方程为 与
与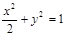 联立,结合根与系数的关系以及判别式得到
联立,结合根与系数的关系以及判别式得到 再由
再由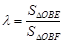
得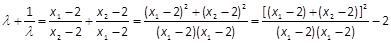 ,即可
,即可
(1)由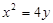 得
得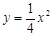 , ∴
, ∴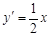 .∴直线
.∴直线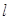 的斜率为
的斜率为 ,
,
故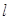 的方程为
的方程为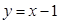 ,∴点A的坐标为(1,0). (2分)
,∴点A的坐标为(1,0). (2分)
设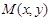 ,则
,则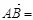 (1,0),
(1,0),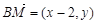 ,
, ,由
,由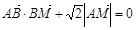
得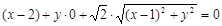 ,整理,得
,整理,得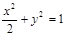 . (4分)
. (4分)
(2)方法一:如图,由题意知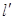 的斜率存在且不为零,设
的斜率存在且不为零,设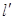 方程为
方程为 ①,将①代入
①,将①代入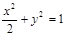 ,整理,得
,整理,得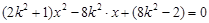 ,设
,设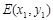 ,
,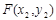 ,则
,则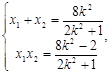 ②
②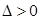 得
得 (7分)
(7分)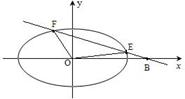
令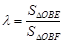 , 则
, 则 ,由此可得
,由此可得 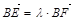 ,
,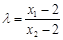 ,且
,且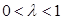 .∴
.∴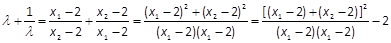
由②知 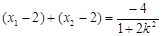 ,
,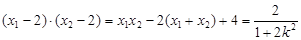 .
.
∴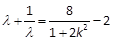 , (10分)
, (10分)
∵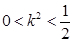 ,∴
,∴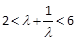 ,解得
,解得 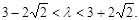 且
且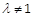 (12分)
(12分)
又∵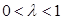 , ∴
, ∴ ,
,
∴△OBE与△OBF面积之比的取值范围是(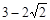 ,1). (13分)
,1). (13分)
方法二:如图,由题意知l’的斜率存在且不为零,设l’ 方程为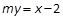 ①,将①代入
①,将①代入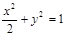 ,整理,得
,整理,得 ,设
,设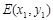 ,
,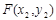 ,则
,则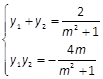 ② ;
② ;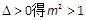 (7分)
(7分)
令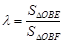 , 则
, 则 ,由此可得
,由此可得 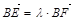

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 :
: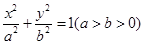 的左焦点
的左焦点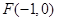 ,离心率为
,离心率为 ,函数
,函数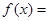
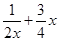 ,
, 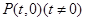 ,
,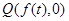 ,过
,过 的直线
的直线 交椭圆
交椭圆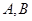 两点,求
两点,求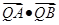 的最小值,并求此时的
的最小值,并求此时的 的值.
的值.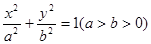 的右焦点为
的右焦点为 ,
, 为上顶点,
为上顶点,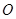 为坐标原点,若△
为坐标原点,若△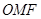 的面积为
的面积为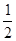 ,且椭圆的离心率为
,且椭圆的离心率为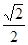 .
. 交椭圆于
交椭圆于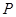 ,
, 两点, 且使点
两点, 且使点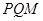 的垂心?若存在,求出直线
的垂心?若存在,求出直线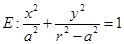 的焦点在
的焦点在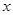 轴上,
轴上, 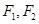 分别是椭圆的左、右焦点,点
分别是椭圆的左、右焦点,点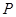 是椭圆在第一象限内的点,直线
是椭圆在第一象限内的点,直线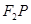 交
交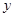 轴于点
轴于点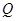 ,
, 时,
时,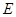 的离心率为
的离心率为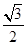 ,求椭圆
,求椭圆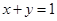 上时,求直线
上时,求直线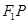 与
与 的夹角;
的夹角;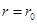 时,若总有
时,若总有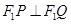 ,猜想:当
,猜想:当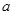 变化时,点
变化时,点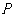 是否在某定直线上,若是写出该直线方程(不必求解过程).
是否在某定直线上,若是写出该直线方程(不必求解过程). +
+ =1(a>b>0)的右焦点,且被圆C所截得的弦长为
=1(a>b>0)的右焦点,且被圆C所截得的弦长为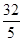 ,点A(3,1)在椭圆E上.
,点A(3,1)在椭圆E上. ·
· 的取值范围.
的取值范围. )2+y2=4,(x-
)2+y2=4,(x-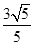 ,
,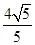 ),F(
),F(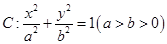 ,称圆心在坐标原点O,半径为
,称圆心在坐标原点O,半径为 的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是
的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是 .
.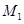 满足
满足 ,求椭圆C及其“伴随圆”的方程;
,求椭圆C及其“伴随圆”的方程; 作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为
作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为 ,求P点的坐标;
,求P点的坐标;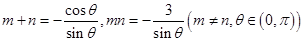 ,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点
,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点 的直线的最短距离
的直线的最短距离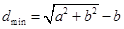 .若存在,求出a,b的值;若不存在,请说明理由.
.若存在,求出a,b的值;若不存在,请说明理由.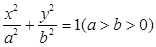 经过点
经过点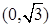 ,离心率为
,离心率为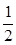 ,左右焦点分别为
,左右焦点分别为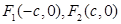 .
.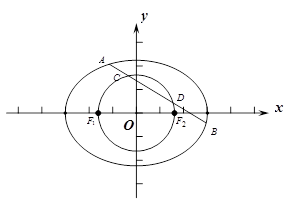
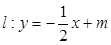 与椭圆交于
与椭圆交于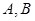 两点,与以
两点,与以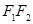 为直径的圆交于
为直径的圆交于 两点,且满足
两点,且满足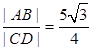 ,求直线
,求直线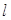 的方程.
的方程. 的方程为
的方程为 ,定直线
,定直线 的方程为
的方程为 .动圆
.动圆 与圆
与圆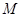 的方程;
的方程; 与轨迹
与轨迹 , 过点
, 过点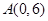 ,并交轨迹
,并交轨迹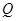 ,求直线
,求直线 的方程及
的方程及 的长.
的长.