题目内容
如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点。

(1)若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正值弦;
(2)用反证法证明:直线ME与BN 是两条异面直线。
(2)用反证法证明:直线ME与BN 是两条异面直线。
| 解:(1)取CD的中点G,连接MG,NG。 设正方形ABCD,DCEF的边长为2, 则MG⊥CD,MG=2,NG=  因为平面ABCD⊥平面DCED, 所以MG⊥平面DCEF, 可得∠MNG是MN与平面DCEF所成的角。 因为MN=  , ,所以sin∠MNG=  则MN与平面DCEF所成角的正弦值为  。 。 |
 |
| (2)假设直线ME与BN共面, 则AB  平面MBEN,且平面MBEN与平面DCEF交于EN 平面MBEN,且平面MBEN与平面DCEF交于EN 由已知,两正方形不共面,故AB  平面DCEF。 平面DCEF。又AB//CD, 所以AB//平面DCEF。 EN为平面MBEN与平面DCEF的交线, 所以AB//EN。 又AB//CD//EF, 所以EN//EF,这与EN∩EF=E矛盾, 故假设不成立。 所以ME与BN不共面,它们是异面直线。 |

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.

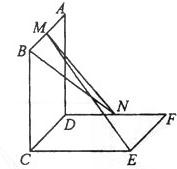 如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.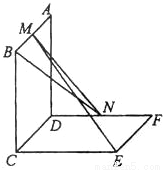 如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.