题目内容
函数f(x)=|log3x|在区间[a,b]上的值域为[0,1],则b-a的最小值为( )
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
分析:因为f(1)=0,所以,1在区间[a,b]上;因为f(3)=1,且f(
)=1,所以,3和
至少有一个在区间[a,b]上.
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:函数f(x)=|log3x|在区间[a,b]上的值域为[0,1],
∵x=1 时,f(x)=0,∵x=3或
时,f(x)=1,
故1∈[a,b],3和
至少有一个在区间[a,b]上,∴b-a的最小值为 1-
=
,
故选B.
∵x=1 时,f(x)=0,∵x=3或
| 1 |
| 3 |
故1∈[a,b],3和
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
故选B.
点评:本题考查函数的值域的应用,由条件知1在区间[a,b]上,3或
至少有一个在区间[a,b]上.
| 1 |
| 3 |

练习册系列答案
相关题目
 )2+7lo
)2+7lo +3≤0的解集为M,求当x∈M时,函数f(x)=(lo
+3≤0的解集为M,求当x∈M时,函数f(x)=(lo )(lo
)(lo )的最大值和最小值.
)的最大值和最小值.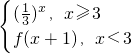 ,则f(2+lo
,则f(2+lo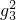 )的值为________.
)的值为________.