题目内容
函数函数f(x)=sin(ωx+φ)(ω>0,|φ|<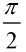
)的最小正周期是π,若其图像向右平移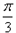 个单位后得到的函数为奇函数,则函数f(x)的图像
个单位后得到的函数为奇函数,则函数f(x)的图像
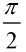
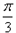 个单位后得到的函数为奇函数,则函数f(x)的图像
个单位后得到的函数为奇函数,则函数f(x)的图像 [ ]
A.关于点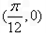 对称
对称
B.关于点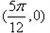 对称
对称
C.关于直线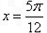 对称
对称
D.关于直线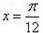 对称
对称
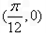 对称
对称 B.关于点
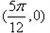 对称
对称C.关于直线
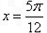 对称
对称 D.关于直线
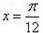 对称
对称C

练习册系列答案
相关题目
 .
. 对不小于2的正整数恒成立,求x的取值范围.
对不小于2的正整数恒成立,求x的取值范围.