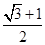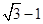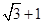题目内容
k为何值时,直线y=kx+2和椭圆 有两个交点 ( )
有两个交点 ( )
A.— <k< <k< | B.k> 或k< — 或k< — |
C.—  k k  | D.k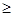  或k 或k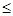 — — |
B
解析试题分析:由 可得 :(2+3k2)x2+12kx+6=0,由△=144k2-24(2+3k2)>0得k>
可得 :(2+3k2)x2+12kx+6=0,由△=144k2-24(2+3k2)>0得k> 或k< —
或k< — ,此时直线和椭圆有两个公共点。
,此时直线和椭圆有两个公共点。
考点:直线与椭圆的位置关系。
点评:判断直线和椭圆交点个数的主要方法,联立方程组,消元,判断△>0、△=0还是△<0。

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知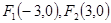 ,动点
,动点 满足:
满足: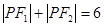 ,则动点
,则动点 的轨迹为( )
的轨迹为( )
| A.椭圆 | B.双曲线 | C.抛物线 | D.线段 |
抛物线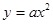 的焦点坐标为
的焦点坐标为
A.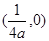 | B.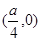 | C. | D.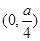 |
已知椭圆 =1双曲线
=1双曲线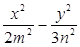 =1有公共的焦点,那么双曲线的渐近线方程是( )
=1有公共的焦点,那么双曲线的渐近线方程是( )
A.x=± | B.y=± | C.x=± | D.y=± |
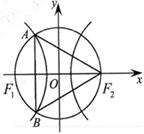
如图,A,B,C分别为 的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )
的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )
A.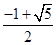 | B.1-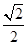 | C.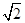 -1 -1 | D.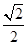 |
已知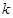 <4,则曲线
<4,则曲线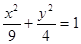 和
和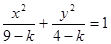 有 ( )
有 ( )
| A.相同的准线 | B.相同的焦点 |
| C.相同的离心率 | D.相同的长轴 |
已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,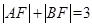 ,则线段AB的中点到y轴的距离为
,则线段AB的中点到y轴的距离为
A.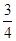 | B.1 | C.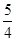 | D.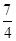 |
直线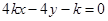 与抛物线
与抛物线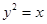 交于
交于 、
、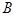 两点,若
两点,若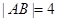 ,则弦
,则弦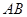 的中点到直线
的中点到直线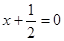 的距离等于( )
的距离等于( )
A.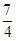 | B.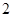 | C. | D. |
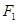 和
和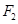 分别是双曲线
分别是双曲线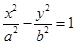 (
(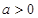 ,
,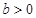 )的两个焦点,A和B是以O为圆心,以
)的两个焦点,A和B是以O为圆心,以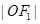 为半径的圆与该双曲线左支的两个交点,且
为半径的圆与该双曲线左支的两个交点,且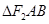 是等边三角形,则该双曲线的离心率为
是等边三角形,则该双曲线的离心率为