题目内容
两个变量x,y与其线性相关系数r有下列说法
(1)若r>0,则x增大时,y也相应增大;
(2)若|r|越趋近于1,则x, y线性相关程度越强;
(3)若r=1或r=-1,则x与y的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上,其中正确的有( )
| A.①② | B.②③ | C.①③ | D.①②③ |
D
解析试题分析:根据相关系数的定义,变量之间的相关关系可利用相关系数r进行判断:
当r为正数时,表示变量x,y正相关,说明一变量随另一变量增减而增减,方向相同;当r为负数时,表示两个变量x,y负相关,|r|越接近于1,相关程度越强;|r|越接近于0,相关程度越弱,故可知①②③正确.
故选D.
考点:线性相关、相关系数。
点评:简单题,当r为正数时,表示变量x,y正相关;当r为负数时,表示两个变量x,y负相关; 的绝对值越接近1,表明两个变量的线性相关性越强; 的绝对值接近于0时,表明两个变量之间几乎不存在线性相关关系.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②一个命题的逆命题正确,此命题的否命题不一定正确;
③线性回归方程 必过点
必过点 ;
;
④设随机变量 且
且 ,则实数
,则实数
⑤  ,使得
,使得 成立
成立
其中错误的个数是( )
| A.1 | B.2 | C.3 | D.4 |
有一个容量为 的样本,其频率分布直方图如图所示,据图估计,样本数据在
的样本,其频率分布直方图如图所示,据图估计,样本数据在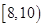 内的频数为
内的频数为
| A.38 | B.57 |
| C.76 | D.95 |
工人月工资y(元)与劳动生产率x(千元)变化的回归方程 ,下列判断正确的是 ( )
,下列判断正确的是 ( )
①劳动生产率为1千元时,工资约为130元
②劳动生产率提高1千元时,月工资约提高80元
③劳动生产率提高1千元时,月工资约提高130元
④当月工资为210元时,劳动生产率约为2千元
| A.① ② | B.① ② ④ | C.② ④ | D.① ② ③ ④ |
在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( )
| A.总偏差平方和 | B.残差平方和 | C.回归平方和 | D.相关指数R2 |
根据一组样本数据 的散点图分析存在线性相关关系,求得其回归方程
的散点图分析存在线性相关关系,求得其回归方程 ,则在样本点
,则在样本点 处的残差为( )
处的残差为( )
A. | B.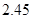 | C. | D. |
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的
列联表:
| | 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
 算得,
算得,
附表:
 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
 有99%以上的把握认为“爱好该项运动与性别有关”
有99%以上的把握认为“爱好该项运动与性别有关” 有99%以上的把握认为“爱好该项运动与性别无关”
有99%以上的把握认为“爱好该项运动与性别无关” 在犯错误的概率不超过0.1%的前提下,认为 “爱好该项运动与性别有关”
在犯错误的概率不超过0.1%的前提下,认为 “爱好该项运动与性别有关”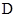 在犯错误的概率不超过0.1%的前提下,认为 “爱好该项运动与性别无关”
在犯错误的概率不超过0.1%的前提下,认为 “爱好该项运动与性别无关” 下列对一组数据的分析,不正确的说法是
| A.数据极差越小,样本数据分布越集中、稳定 |
| B.数据平均数越小,样本数据分布越集中、稳定 |
| C.数据标准差越小,样本数据分布越集中、稳定 |
| D.数据方差越小,样本数据分布越集中、稳定 |
 次测评中的成绩由右边茎叶图表示(均为整数),其中有一个数字无法看清,现用字母
次测评中的成绩由右边茎叶图表示(均为整数),其中有一个数字无法看清,现用字母 代替,则甲的平均成绩超过乙的平均成绩的概率为( ).
代替,则甲的平均成绩超过乙的平均成绩的概率为( ).



