题目内容
在计算机的算法语言中有一种函数[x]叫做取整函数(也称高斯函数),它表示x的整数部分,即[x]是不超过x的最大整数.例如:[2]=2,[3.1]=3,[-2.6]=-3.设函数f(x)=
-
,则函数y=[f(x)]+[f(-x)]的值域为
______.
| 2x |
| 1+2x |
| 1 |
| 2 |
由题意,f(x)=
-
=1-
-
=
-
;f(-x)=
-
=
-
;
∴f(-x)=-f(x),即f(x)是奇函数.
又∵2x>0,∴1+2x>1,∴0 <
< 1,∴-
<
-
<
;
即-
<f(-x)<
.所以,-
<f(x)<
.
当x=0时,f(x)=f(-x)=0,y=[f(x)]+[f(-x)]=0;
当x≠0时,若x>0,则0<f(x)<
,-
<f(-x)<0,
∴y=[f(x)]+[f(-x)]=0+(-1)=-1,
若x<0,则y=[f(x)]+[f(-x)]=(-1)+0=-1.
所以函数y的值域为{0,-1}.
故答案为:{0,-1}
| 2x |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 1+2x |
| 2-x |
| 1+2-x |
| 1 |
| 2 |
| 1 |
| 1+2x |
| 1 |
| 2 |
∴f(-x)=-f(x),即f(x)是奇函数.
又∵2x>0,∴1+2x>1,∴0 <
| 1 |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 2 |
即-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x=0时,f(x)=f(-x)=0,y=[f(x)]+[f(-x)]=0;
当x≠0时,若x>0,则0<f(x)<
| 1 |
| 2 |
| 1 |
| 2 |
∴y=[f(x)]+[f(-x)]=0+(-1)=-1,
若x<0,则y=[f(x)]+[f(-x)]=(-1)+0=-1.
所以函数y的值域为{0,-1}.
故答案为:{0,-1}

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
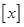 叫做取整函数(也叫高斯函数).它表示x的整数部分,即表示不超过x的最大整数.如
叫做取整函数(也叫高斯函数).它表示x的整数部分,即表示不超过x的最大整数.如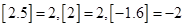 .设函数
.设函数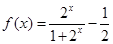 ,则函数
,则函数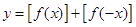 的值域为 .
的值域为 .