题目内容
已知f（x）是二次函数，满足f（x+1）+f（2x-1）=-5x2-x，求函数f（x）的解析式、值域，并写出函数的单调递减区间．
解：根据题意设f（x）=ax2+bx+c（a≠0），
所以f（x+1）+f（2x-1）=5ax2+（3b-2a）x+2（a+c）=-5x2-x，
∴
，解得
，
∴f（x）=-x2-x+1，
所以函数图象开口向下，最大值在x=
处取得，为
，故值域为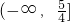
，
单调递减区间为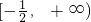
．
分析：先利用待定系数法求出函数的解析式，再判断函数的单调性，最后求出最值．
点评：本题考察待定系数法求函数的解析式，以及二次函数的单调性和值域，属基础题．
所以f（x+1）+f（2x-1）=5ax2+（3b-2a）x+2（a+c）=-5x2-x，
∴
，解得，∴f（x）=-x2-x+1，
所以函数图象开口向下，最大值在x=
处取得，为，故值域为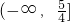，单调递减区间为
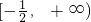．分析：先利用待定系数法求出函数的解析式，再判断函数的单调性，最后求出最值．
点评：本题考察待定系数法求函数的解析式，以及二次函数的单调性和值域，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目