题目内容
已知函数y=f(x)是定义在实数集R上的奇函数,且当x>0,f(x)+xf′(x)>0(其中f′(x)是f(x)的导函数),a={ 4}f
4}f 4,b=
4,b= f(
f( )设c=(lg
)设c=(lg ),则a,b,c的大小关系是( )
),则a,b,c的大小关系是( )A.c>a>b
B.c>b>a
C.a>b>c
D.a>c>b
【答案】分析:我们可以令函数F(x)=xf(x),证明其为偶函数,再研究其单调性,分别求出a,b,c,再利用F(x)的单调性进行判断;
解答:解:令函数F(x)=xf(x),则函数
f(-x)=-f(x)
∴F(-x)=F(x),
F(x)=xf(x)为偶函数.
当x>0时,F′(x)=f(x)+xf′(x)>0,此时函数递增,
则 ,
,
 ,
,
 ,
,
因为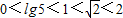 ,
,
所以a>b>c,
故选C.
点评:此题主要考查对数函数的性质及其图象,以及利用函数的单调性进行比较数的大小关系,是一道基础题;
解答:解:令函数F(x)=xf(x),则函数
f(-x)=-f(x)
∴F(-x)=F(x),
F(x)=xf(x)为偶函数.
当x>0时,F′(x)=f(x)+xf′(x)>0,此时函数递增,
则
 ,
, ,
, ,
,因为
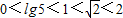 ,
,所以a>b>c,
故选C.
点评:此题主要考查对数函数的性质及其图象,以及利用函数的单调性进行比较数的大小关系,是一道基础题;

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足