题目内容
已知函数f（x）=log2(x2-ax-a)在区间（-∞,1-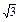
］上是单调递减函数.求实数a的取值范围.
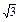］上是单调递减函数.求实数a的取值范围.a的取值范围是{a|2-2
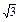≤a＜2}令g(x)=x2-ax-a,则g(x)=（x-
）2-a-
,由以上知g(x）的图象关于直线x=
对称且此抛物线开口向上.因为函数f(x)=log2g(x)的底数2＞1,
在区间（-∞,1-
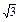］上是减函数，所以g(x)=x2-ax-a在区间（-∞,1-
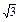］上也是单调减函数，且g(x)＞0.∴
解得2-2
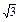≤a＜2.故a的取值范围是{a|2-2
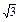≤a＜2}.
练习册系列答案
相关题目
，且
，
，
，
三数大小关系为（ ）
，
，
，
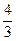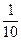时所对应的图象，则相应于C1，C2，C3，C4的a的值依次是( )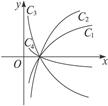
，且
求实数
的取值范围．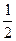
<1,那么a的取值范围是（ ）
log85 
log2516 + log324 .
，
，且
，则
的最大值是______________。