题目内容

设x1、x2是函数f(x)=ex定义域内的两个变量，x1＜x2,若α=(x1+x2),那么下列不等式恒成立的是(    )

A.|f(α)-f(x1)|＞|f(x2)-f(α)|                 

B.|f(α)-f(x1)|＜|f(x2)-f(α)|

C.|f(α)-f(x1)|=|f(x2)-f(α)|                 

D.f(x1)f(x2)＞f2(α)

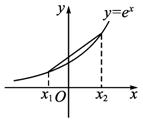
解析：如图f(x)为增函数，

∵x1＜x2,α=(x1+x2),

∴x1＜α＜x2,∴f(x1)＜f(α)＜f(x2).

∵f()＜［f(x1)+f(x2)］,即2f(α)＜f(x1)+f(x2).

∴f(α)-f(x1)＜f(x2)-f(α).

    即|f(α)-f(x1)|＜|f(x2)-f(α)|.

答案：B


练习册系列答案
相关题目
设x1，x2是函数f(x)=
a
3
x3+
b
2
x2-a2x(a＞0)的两个极值点，且|x1|+|x2|=2．
（1）证明：|b|≤
4
3
9
．
（2）若g（x）=f'（x）-2a（x-x1），证明当x1＜x＜2时，且x1＜0时，|g（x）|≤4a．
设x1，x2是函数f（x）=
a
3
x3+
b
2
x2-a2x（a＞0）的两个极值点，且|x1|+|x2|=2．
（1）求a的取值范围；
（2）求证：|b|≤
4
3
9
．
设函数f（x）=x2+bx+c，且f（1）=-
12
．
（1）求证：函数f（x）有两个零点．
（2）设x1、x2是函数f（x）的两个零点，求|x1-x2|的取值范围．
（3）求证：函数f（x）在区间（0，2）内至少有一个零点．
已知函数f（x）=ax2+bx+c，且f(1)=-
a
2
，3a＞2c＞2b．
（1）求证：a＞0且-3＜
b
a
＜-
3
4
；
（2）求证：函数f（x）在区间（0，2）内至少有一个零点；
（3）设x1，x2是函数f（x）的两个零点，求|x1-x2|的范围．
设x1，x2是函数f（x）=x3-2ax2+a2x的两个极值点，若x1＜2＜x2，则实数a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网