题目内容
 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
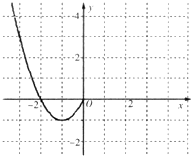
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x. (Ⅰ)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(Ⅱ)写出函数f(x)的解析式和值域;
(Ⅲ)若f(a+1)=(a+1)(a-1),求a的取值集合.
分析:(I)根据偶函数的图象关于y轴对称,由已知中数f(x)在y轴左侧的图象,可得完整函数f(x)的图象,根据函数图象从左到右上升的部分对应函数的增区间,可得函数f(x)的增区间;
(Ⅱ)由当x≤0时,f(x)=x2+2x,x>0时,-x<0,由偶函数的定义,可得x>0时的函数解析式,综合两个情况可得函数的解析式
(III)结合(II)中函数的解析式,结合f(a+1)=(a+1)(a-1),可构造关于a的方程组,进而结合绝对值的性质,求出a的取值范围.
(Ⅱ)由当x≤0时,f(x)=x2+2x,x>0时,-x<0,由偶函数的定义,可得x>0时的函数解析式,综合两个情况可得函数的解析式
(III)结合(II)中函数的解析式,结合f(a+1)=(a+1)(a-1),可构造关于a的方程组,进而结合绝对值的性质,求出a的取值范围.
解答:解:(Ⅰ)根据偶函数的图象关于y轴对称,可得函数f(x)的图象如下图所示:
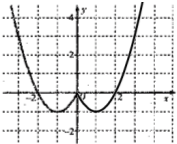
由图象可知函数f(x)单调增区间是(-1,0),(1,+∞)(4分)
(Ⅱ)∵当x≤0时,f(x)=x2+2x
∴当x>0时,-x<0,
则f(-x)=(-x)2+2•(-x)=x2-2x
又∵函数f(x)是定义在R上的偶函数,
∴f(x)=f(-x)=x2-2x
综上,当x∈R时,f(x)=x2-2|x|…(6分)
由图象可得函数的值域为[-1,+∞)…(8分)
(Ⅲ)由f(a+1)=(a+1)(a-1),及f(x)=x2-2|x|得
(a+1)2-2|a+1|=(a+1)(a-1),
即|a+1|=a+1
即a+1≥0
解得a≥-1
故a的取值集合是[-1,+∞)…(12分)

由图象可知函数f(x)单调增区间是(-1,0),(1,+∞)(4分)
(Ⅱ)∵当x≤0时,f(x)=x2+2x
∴当x>0时,-x<0,
则f(-x)=(-x)2+2•(-x)=x2-2x
又∵函数f(x)是定义在R上的偶函数,
∴f(x)=f(-x)=x2-2x
综上,当x∈R时,f(x)=x2-2|x|…(6分)
由图象可得函数的值域为[-1,+∞)…(8分)
(Ⅲ)由f(a+1)=(a+1)(a-1),及f(x)=x2-2|x|得
(a+1)2-2|a+1|=(a+1)(a-1),
即|a+1|=a+1
即a+1≥0
解得a≥-1
故a的取值集合是[-1,+∞)…(12分)
点评:本题考查的知识点是函数解析式的求法,函数的奇偶性,函数的单调性,函数的值域,函数的综合应用,是函数图象和性质的简单综合问题,难度中档.

练习册系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+