题目内容
如图，已知α∩β=a，β∩γ=b，γ∩α=c，a∥b,求证：a∥c.
思路解析：由a∥γ可得a∥r，而c是过a的平面α与γ的交线,由线面平行的性质定理易得结论成立.
证明：因为β∩γ=b，a∥b，所以a∥γ.
因为α∩γ=c,a
α，所以a∥c.
练习册系列答案
相关题目
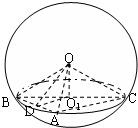如图，已知A，B，C是表面积为48π的球面上的三点，AB=2，BC=4，∠ABC=60°，O为球心，则二面角O-AB-C的大小为：（ ）A、
| ||||
B、
| ||||
C、arccos
| ||||
D、arccos
|
17、如图，已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆（x-1）2+y2=1的交点，则|AB|•|CD|=
如图，已知A（0，5），B（1，1），C（3，2），D（4，3），动点P（x，y）所在的区域为四边形ABCD（含边界）．若目标函数z=ax+y只在点D处取得最优解，则实数a的取值范围是
如图，已知∠A=60°，P、Q分别是∠A两边上的动点．
（2012•江苏二模）如图，已知A、B是函数y=3sin（2x+θ）的图象与x轴两相邻交点，C是图象上A，B之间的最低点，则