题目内容
设曲线 在点(3,
在点(3, )处的切线与直线ax+y+1=0垂直,则a=________.
)处的切线与直线ax+y+1=0垂直,则a=________.
-4
分析:先求出函数的导数,再求出在已知点出的斜率,根据直线垂直斜率之积为-1,求出a的值.
解答:∵ ,∴y′=-
,∴y′=-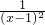 ,
,
∴在点(3, )处的切线的斜率为:
)处的切线的斜率为: ,
,
∵切线与直线ax+y+1=0垂直,∴a=4,
故答案为:-4.
点评:本题考查了导数的几何意义,以及直线垂直的等价条件的应用.
分析:先求出函数的导数,再求出在已知点出的斜率,根据直线垂直斜率之积为-1,求出a的值.
解答:∵
 ,∴y′=-
,∴y′=-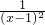 ,
,∴在点(3,
 )处的切线的斜率为:
)处的切线的斜率为: ,
,∵切线与直线ax+y+1=0垂直,∴a=4,
故答案为:-4.
点评:本题考查了导数的几何意义,以及直线垂直的等价条件的应用.

练习册系列答案
相关题目
 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则a=( )
垂直,则a=( ) D.
D. 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则
垂直,则
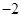 C.
C.
 D.
D.

 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则
垂直,则
 C.
C.
 D.
D.

 在点(3,
在点(3, )处的切线与直线ax+y+1=0垂直,则a=( ).
)处的切线与直线ax+y+1=0垂直,则a=( ).