题目内容
 设全集U是实数集R,M={x|x2>4},N={x|1<x≤3},则图中阴影部分表示的集合是( )
设全集U是实数集R,M={x|x2>4},N={x|1<x≤3},则图中阴影部分表示的集合是( )分析:先求出集合M,再根据韦恩图得到阴影部分表示的集合为N∩(CUM),借助数轴即可得解
解答:解:M={x|x2>4}={x|x<-2或x>2}
由韦恩图知阴影部分表示的集合为N∩(CUM)
又CUM={x|-2≤x≤2},N={x|1<x≤3}
∴N∩(CUM)={x|1<x≤2}
故选C
由韦恩图知阴影部分表示的集合为N∩(CUM)
又CUM={x|-2≤x≤2},N={x|1<x≤3}
∴N∩(CUM)={x|1<x≤2}
故选C
点评:本题考查韦恩图与集合运算,要求会读韦恩图,会在数轴上进行集合运算.属简单题

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 设全集U是实数集R,M={x|x2>4},N={x|
设全集U是实数集R,M={x|x2>4},N={x|| 2 |
| x-1 |
| A、{x|-2≤x<1} |
| B、{x|-2≤x≤2} |
| C、{x|1<x≤2} |
| D、{x|x<2} |
 设全集U是实数集R,M={x||x|≥2},N={x|1<x<3},则图中阴影部分所表示的集合是( )
设全集U是实数集R,M={x||x|≥2},N={x|1<x<3},则图中阴影部分所表示的集合是( )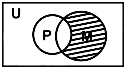 设全集U是实数集R,M={x|x<-1,或x>2},P={x|x<1或x>5},则图中阴部分所表示的集合是( )
设全集U是实数集R,M={x|x<-1,或x>2},P={x|x<1或x>5},则图中阴部分所表示的集合是( ) 设全集U是实数集R,
设全集U是实数集R, (2010•台州一模)设全集U是实数集R,M={x|x2>4},N={x|y=lg(x2-4x+3)},则图中阴影部分所表示的集合是
(2010•台州一模)设全集U是实数集R,M={x|x2>4},N={x|y=lg(x2-4x+3)},则图中阴影部分所表示的集合是