题目内容
15.过点(5,3)且与直线2x-3y-7=0平行的直线方程是( )| A. | 3x+2y-21=0 | B. | 2x-3y-1=0 | C. | 3x-2y-9=0 | D. | 2x-3y+9=0 |
分析 求出直线的斜率,利用点斜式求解直线方程即可.
解答 解:过点(5,3)且与直线2x-3y-7=0平行的直线的斜率为:$\frac{2}{3}$,
所求直线方程为:y-3=$\frac{2}{3}$(x-5).
即2x-3y-1=0.
故选:B.
点评 本题考查直线方程的求法,平行线的应用,考查计算能力.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
3.设集合M={x|(x+3)(x-2)<0,x∈R},N={0,1,2},则M∩N=( )
| A. | {0,1,2} | B. | {0,1} | C. | {x|0<x<2} | D. | {x|-3<x<2} |
20.利用计算机产生0~3之间的均匀随机数a、x,则事件“logax>0(a>0且a≠≠1)”发生的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{9}$ | D. | $\frac{5}{9}$ |
7.若向量$\overrightarrow{a}$=(3,m),$\overrightarrow{b}$=(2,-1),$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数m的值为( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 6 |
4.为了分流地铁高峰的压力,某市发改委通过听众会,决定实施低峰优惠票价制度.不超过22公里的地铁票价如下表:
现有甲、乙两位乘客,他们乘坐的里程都不超过22公里.已知甲、乙乘车不超过6公里的概率分别为$\frac{1}{4}$,$\frac{1}{3}$,甲、乙乘车超过6公里且不超过12公里的概率分别为$\frac{1}{2}$,$\frac{1}{3}$.
(Ⅰ)求甲、乙两人所付乘车费用不相同的概率;
(Ⅱ)设甲、乙两人所付乘车费用之和为随机变量ξ,求ξ的分布列与数学期望.
| 乘坐里程x(单位:km) | 0<x≤6 | 6<x≤12 | 12<x≤22 |
| 票价(单位:元) | 3 | 4 | 5 |
(Ⅰ)求甲、乙两人所付乘车费用不相同的概率;
(Ⅱ)设甲、乙两人所付乘车费用之和为随机变量ξ,求ξ的分布列与数学期望.
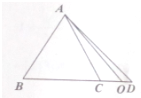 如图,在△ABC中,点D是BC延长线上的点,$\overline{BC}$=3$\overline{CD}$,O在线段CD上且不与端点重合,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+(1-x)$\overrightarrow{AC}$,则x的取值范围是($-\frac{1}{3}$,0).
如图,在△ABC中,点D是BC延长线上的点,$\overline{BC}$=3$\overline{CD}$,O在线段CD上且不与端点重合,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+(1-x)$\overrightarrow{AC}$,则x的取值范围是($-\frac{1}{3}$,0).