Question

已知函数f（x）=2sin（

π

3

-2x）
1）用五点法作出函数在一个周期内的图象；
2）求函数的周期和单增区间；
3）若方程f（x）=a在区间（0，

2π

3

）有两个不同的实根，求a的范围．

Answer 1

分析：（1）分别令2x-

π

3

=0、

π

2

、π、

3π

2

、2π，可得x=

π

6

、

5π

12

、

2π

3

、

11π

12

、

7π

6

，由此得到函数在一个周期内图象上的关键的点，描出这五个点的坐标再连成平滑的曲线，即可得到函数在一个周期内的图象．
（2）根据三角函数的单调区间的公式与周期公式加以计算，可得函数的周期和单增区间；
（3）研究f（x）区间（0，

2π

3

）上的单调性与函数的取值，可得f（x）在区间（

π

6

，

2π

3

）上且x≠

5π

12

时，有两个x对应一个函数值y，由此即可算出满足条件的实数a的范围．

解答：解：（1）函数f（x）=2sin（

π

3

-2x）=-2sin（2x-

π

3

）．列出如下表格：

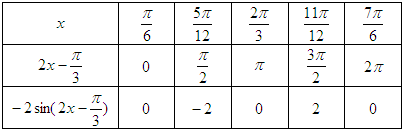
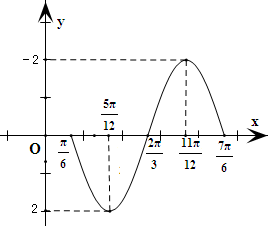
在直角坐标系中描出点（

π

6

，0），（

5π

12

，-2），（

2π

3

，0），（

11π

12

，2），（

7π

6

，0）．
将此五个点连成平滑的曲线，即得函数f（x）=2sin（

π

3

-2x）在一个周期内的图象，如图所示；
（2）∵f（x）=2sin（

π

3

-2x）=-2sin（2x-

π

3

）．∴函数的周期T=

2π

2

=π，
令

π

2

+2kπ≤2x-

π

3

≤

3π

2

+2kπ（k∈Z），得

5π

12

+kπ≤x≤

11π

12

+kπ（k∈Z），
∴函数的单调递增区间为[

5π

12

+kπ，

11π

12

+kπ]（k∈Z）．
（3）当x∈（0，

2π

3

）时，可得f（x）=2sin（

π

3

-2x）在（0，

5π

12

]上为减函数，函数值从

3

减小到-2；
在[

5π

12

，

2π

3

）上为增函数，函数值从-2增大到0．（x=0与

2π

3

处的函数值取不到）
∴函数f（x）=2sin（

π

3

-2x）在区间（

π

6

，

2π

3

）上且x≠

5π

12

时，有两个x对应一个函数值y．
因此，方程f（x）=a在区间（0，

2π

3

）有两个不同的实根，a的取值范围为（-2，0）．

点评：本题给出正弦型三角函数，求它的单调区间并作出一个周期内的图象，讨论关于x的方程解的个数，着重考查了三角函数的单调性、三角函数的图象作法与函数图象的变换公式等知识，属于中档题．