题目内容
已知点A(1,1),B(1,-1),C(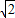 cosθ,
cosθ,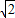 sinθ)(θ∈R),O为坐标原点.
sinθ)(θ∈R),O为坐标原点.(1)若|
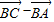 |=
|=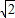 ,求sin2θ的值;
,求sin2θ的值;(2)若实数m,n满足m
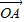 +n
+n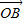 =
=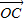 ,求(m-3)2+n2的最大值.
,求(m-3)2+n2的最大值.
【答案】分析:(1)根据向量的坐标计算(终点坐标减始点坐标)求出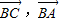 ,然后再根据向量减法和模的坐标计算结合条件|
,然后再根据向量减法和模的坐标计算结合条件|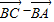 |=
|=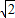 得出sinθ+cosθ=
得出sinθ+cosθ=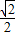 再两边平方即可得解.
再两边平方即可得解.
(2)根据向量相等和条件m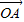 +n
+n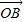 =
=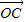 求出
求出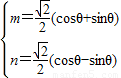 然后再代入(m-3)2+n2中可得(m-3)2+n2=-3
然后再代入(m-3)2+n2中可得(m-3)2+n2=-3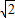 (sinθ+cosθ)+10再结合辅助角公式可得(m-3)2+n2=-6sin(θ+
(sinθ+cosθ)+10再结合辅助角公式可得(m-3)2+n2=-6sin(θ+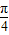 )+10从而可得出当sin(θ+
)+10从而可得出当sin(θ+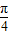 )=-1时,(m-3)2+n2取得最大值16.
)=-1时,(m-3)2+n2取得最大值16.
解答:解:(1)∵|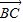 -
-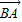 |=|
|=|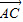 |,A(1,1),B(1,-1),C(
|,A(1,1),B(1,-1),C(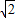 cosθ,
cosθ,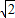 sinθ)
sinθ)
∴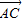 =(
=(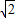 cosθ-1,
cosθ-1,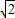 sinθ-1)
sinθ-1)
∴|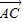 |2=(
|2=(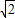 cosθ-1)2+(
cosθ-1)2+(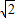 sinθ-1)2=-2
sinθ-1)2=-2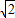 (sinθ+cosθ)+4.
(sinθ+cosθ)+4.
∴-2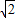 (sinθ+cosθ)+4=2,即sinθ+cosθ=
(sinθ+cosθ)+4=2,即sinθ+cosθ=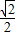 ,
,
两边平方得1+sin2θ= ,
,
∴sin2θ=- .
.
(2)由已知得:(m,m)+(n,-n)=(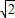 cosθ,
cosθ,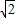 sinθ),
sinθ),
∴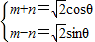
解得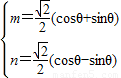
∴(m-3)2+n2=m2+n2-6m+9,
=-3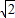 (sinθ+cosθ)+10
(sinθ+cosθ)+10
=-6sin(θ+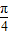 )+10,
)+10,
∴当sin(θ+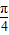 )=-1时,(m-3)2+n2取得最大值16.
)=-1时,(m-3)2+n2取得最大值16.
点评:本题主要考察了向量的坐标计算、减法、模的坐标计算以及三角函数的化简求值,属常考题型,较难.解题的关键是掌握常用的变形技巧:通过sinθ cosθ两边平方求出sin2θ:通过辅助角公式可将-3
cosθ两边平方求出sin2θ:通过辅助角公式可将-3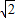 (sinθ+cosθ)+10化为-6sin(θ+
(sinθ+cosθ)+10化为-6sin(θ+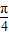 )+10!
)+10!
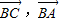 ,然后再根据向量减法和模的坐标计算结合条件|
,然后再根据向量减法和模的坐标计算结合条件|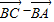 |=
|=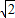 得出sinθ+cosθ=
得出sinθ+cosθ=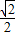 再两边平方即可得解.
再两边平方即可得解.(2)根据向量相等和条件m
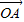 +n
+n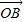 =
=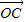 求出
求出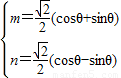 然后再代入(m-3)2+n2中可得(m-3)2+n2=-3
然后再代入(m-3)2+n2中可得(m-3)2+n2=-3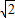 (sinθ+cosθ)+10再结合辅助角公式可得(m-3)2+n2=-6sin(θ+
(sinθ+cosθ)+10再结合辅助角公式可得(m-3)2+n2=-6sin(θ+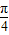 )+10从而可得出当sin(θ+
)+10从而可得出当sin(θ+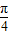 )=-1时,(m-3)2+n2取得最大值16.
)=-1时,(m-3)2+n2取得最大值16.解答:解:(1)∵|
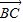 -
-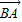 |=|
|=|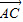 |,A(1,1),B(1,-1),C(
|,A(1,1),B(1,-1),C(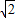 cosθ,
cosθ,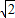 sinθ)
sinθ)∴
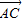 =(
=(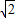 cosθ-1,
cosθ-1,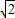 sinθ-1)
sinθ-1)∴|
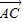 |2=(
|2=(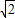 cosθ-1)2+(
cosθ-1)2+(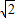 sinθ-1)2=-2
sinθ-1)2=-2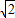 (sinθ+cosθ)+4.
(sinθ+cosθ)+4.∴-2
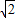 (sinθ+cosθ)+4=2,即sinθ+cosθ=
(sinθ+cosθ)+4=2,即sinθ+cosθ=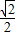 ,
,两边平方得1+sin2θ=
 ,
,∴sin2θ=-
 .
.(2)由已知得:(m,m)+(n,-n)=(
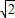 cosθ,
cosθ,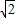 sinθ),
sinθ),∴
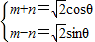
解得
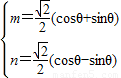
∴(m-3)2+n2=m2+n2-6m+9,
=-3
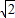 (sinθ+cosθ)+10
(sinθ+cosθ)+10=-6sin(θ+
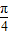 )+10,
)+10,∴当sin(θ+
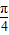 )=-1时,(m-3)2+n2取得最大值16.
)=-1时,(m-3)2+n2取得最大值16.点评:本题主要考察了向量的坐标计算、减法、模的坐标计算以及三角函数的化简求值,属常考题型,较难.解题的关键是掌握常用的变形技巧:通过sinθ
 cosθ两边平方求出sin2θ:通过辅助角公式可将-3
cosθ两边平方求出sin2θ:通过辅助角公式可将-3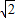 (sinθ+cosθ)+10化为-6sin(θ+
(sinθ+cosθ)+10化为-6sin(θ+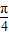 )+10!
)+10! 
练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 在平面直角坐标系xoy中,已知点A(-1,1),P是动点,且△POA的三边所在直线的斜率满足kOP+kOA=kPA
在平面直角坐标系xoy中,已知点A(-1,1),P是动点,且△POA的三边所在直线的斜率满足kOP+kOA=kPA