题目内容
已知圆C:(x+3)2+y2=4,P为圆C上任一点,A(3,0)为定点,AP的中点为M.
求:
(1)动点M的轨迹方程;
(2)动点M的轨迹与圆C的公切线方程.
求:
(1)动点M的轨迹方程;
(2)动点M的轨迹与圆C的公切线方程.
分析:(1)由圆C:(x+3)2+y2=4,P为圆C上任一点,知P(-3+2cosθ,2sixθ),设AP的中点M(x,y),由A(3,0),利用中点坐标公式能求出动点M的轨迹方程.
(2)动点M的轨迹是以M(0,0)为圆心,以1为半径的圆,设BD是圆M与圆C的公切线,D和B是切点,则BC=2,MD=1,MC=3,设BD交x轴于E,则E(3,0),故tan∠BEC=
,由此能求出动点M的轨迹与圆C的公切线方程.
(2)动点M的轨迹是以M(0,0)为圆心,以1为半径的圆,设BD是圆M与圆C的公切线,D和B是切点,则BC=2,MD=1,MC=3,设BD交x轴于E,则E(3,0),故tan∠BEC=
| ||
| 4 |
解答:解:(1)∵圆C:(x+3)2+y2=4,P为圆C上任一点,
∴P(-3+2cosθ,2sixθ),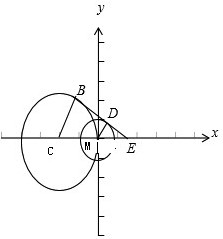
设AP的中点M(x,y),
∵A(3,0),∴
,(0≤θ<2π)
∴x2+y2=1.
(2)如图,动点M的轨迹是以M(0,0)为圆心,以1为半径的圆,
设BD是圆M与圆C的公切线,D和B是切点,则BC=2,MD=1,MC=3,
设BD交x轴于E,则E(3,0),
∴tan∠BEC=
=
=
,
∴动点M的轨迹与圆C的公切线方程为:y=±
(x-3).
∴P(-3+2cosθ,2sixθ),

设AP的中点M(x,y),
∵A(3,0),∴
|
∴x2+y2=1.
(2)如图,动点M的轨迹是以M(0,0)为圆心,以1为半径的圆,
设BD是圆M与圆C的公切线,D和B是切点,则BC=2,MD=1,MC=3,
设BD交x轴于E,则E(3,0),
∴tan∠BEC=
| 2 | ||
|
| 2 | ||
4
|
| ||
| 4 |
∴动点M的轨迹与圆C的公切线方程为:y=±
| ||
| 4 |
点评:本题考查点的轨迹方程的求法,考查两个圆的公切线方程的求法.解题时要认真审题,仔细解答,注意圆的参数方程和中点坐标公式的灵活运用.

练习册系列答案
相关题目
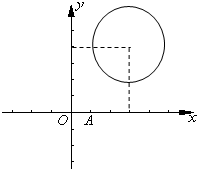 已知圆C:(x-3)2+(y-4)2=4,
已知圆C:(x-3)2+(y-4)2=4,