题目内容
若直线y=x+m与曲线
=x有两个不同的交点，则实数m的取值范围为
- A.（-
，） - B.（-，-1]
- C.（-，1]
- D.[1，）
B
分析：根据题意画出曲线=x的图象，结合圆与直线的位置关系的判定进而得到答案．
解答：
解：由题意可得：曲线=x表示圆的右半圆，即如图所示
当直线y=x+m与圆x2+y2=0相切时，则m=
，
结合图象可得：若直线y=x+m与曲线=x相切时，则m=-．
平移直线y=x可得若直线y=x+m与曲线=x有两个不同的交点，则实数m的取值范围为：（-，-1]．
故选B．
点评：解决此类问题的关键是熟练掌握直线与圆的图象，以及圆与直线位置关系的判定，并且掌握数形结合的数学思想．
分析：根据题意画出曲线
=x的图象，结合圆与直线的位置关系的判定进而得到答案．解答：
解：由题意可得：曲线=x表示圆的右半圆，即如图所示当直线y=x+m与圆x2+y2=0相切时，则m=
，结合图象可得：若直线y=x+m与曲线
=x相切时，则m=-．平移直线y=x可得若直线y=x+m与曲线
=x有两个不同的交点，则实数m的取值范围为：（-，-1]．故选B．
点评：解决此类问题的关键是熟练掌握直线与圆的图象，以及圆与直线位置关系的判定，并且掌握数形结合的数学思想．
练习册系列答案
53随堂测系列答案
相关题目
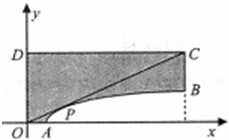已知图形OAPBCD是由不等式组
，|AN|＝3，且|BN|＝6，分别以l1及l2为x轴和y轴，建立如图坐标系，求曲线C的方程．
)为圆心，1为半径的圆相切，又知C的一个焦点与A关于y = x对称．