题目内容
已知f(x)=ax3+bx2+cx的极小值为-4,f′(x)>0的解集是{x|1<x<3}.(1)求f(x)的解析式;
(2)当x∈[2,3]时,求g(x)=f′(x)+6(m-2)x的最大值.
【答案】分析:(Ⅰ)导数f′(x)>0的x的取值范围{x|1<x<3}得到1和3分别为函数的极小值和极大值点即f′(1)=0且f′(3)=0,且有f(1)=-4,三者联立即可求出a、b和c的值,得到f(x)的解析式
(II)求出g(x)=f′(x)+6(m-2)x的解析式,利用二次函数的图象和性质,分类讨论后可得当x∈[2,3]时,求g(x)=f′(x)+6(m-2)x的最大值.
解答:解:(Ⅰ)∵f(x)=ax3+bx2+cx
∴f′(x)=3ax2+2bx+c,a>0,
又∵f′(x)>0的解集是{x|1<x<3}.
∴1,3分别为f(x)的极小值,极大值点,且a>0,
∴f′(1)=0,f′(3)=0,f(1)=-4
∴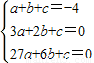 ,
,
解得a=-1,b=6,c=-9,
∴f(x)=-x3+6x2-9x,
(II)g(x)=f′(x)+6(m-2)x
=-3x2+12x-9+6(m-2)x
=-3x2+6mx-9
其图象是开口朝下,且以直线x=m为对称轴的抛物线
当m>3时,g(x)在区间[2,3]上为增函数,
此时当x=3时,g(x)取最大值18m-36
当2≤m≤3时,g(x)在区间[2,m]上为增函数,在区间[m,3]上为减函数,
此时当x=m时,g(x)取最大值3m2-9
当m<2时,g(x)在区间[2,3]上为减函数,
此时当x=2时,g(x)取最大值12m-21
点评:本题考查的知识点是利用导数求区间上函数的极值,求函数的解析式,二次函数在定区间上的最值问题,解答(I)的关键是熟练掌握函数极值点与导数零点的关系,解答(II)的关键是对区间与函数图象对称轴的关系进行分类讨论.
(II)求出g(x)=f′(x)+6(m-2)x的解析式,利用二次函数的图象和性质,分类讨论后可得当x∈[2,3]时,求g(x)=f′(x)+6(m-2)x的最大值.
解答:解:(Ⅰ)∵f(x)=ax3+bx2+cx
∴f′(x)=3ax2+2bx+c,a>0,
又∵f′(x)>0的解集是{x|1<x<3}.
∴1,3分别为f(x)的极小值,极大值点,且a>0,
∴f′(1)=0,f′(3)=0,f(1)=-4
∴
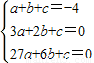 ,
,解得a=-1,b=6,c=-9,
∴f(x)=-x3+6x2-9x,
(II)g(x)=f′(x)+6(m-2)x
=-3x2+12x-9+6(m-2)x
=-3x2+6mx-9
其图象是开口朝下,且以直线x=m为对称轴的抛物线
当m>3时,g(x)在区间[2,3]上为增函数,
此时当x=3时,g(x)取最大值18m-36
当2≤m≤3时,g(x)在区间[2,m]上为增函数,在区间[m,3]上为减函数,
此时当x=m时,g(x)取最大值3m2-9
当m<2时,g(x)在区间[2,3]上为减函数,
此时当x=2时,g(x)取最大值12m-21
点评:本题考查的知识点是利用导数求区间上函数的极值,求函数的解析式,二次函数在定区间上的最值问题,解答(I)的关键是熟练掌握函数极值点与导数零点的关系,解答(II)的关键是对区间与函数图象对称轴的关系进行分类讨论.

练习册系列答案
相关题目
已知F(x)=ax3+bx5+cx3+dx-6,F(-2)=10,则F(2)的值为( )
| A、-22 | B、10 | C、-10 | D、22 |