题目内容
设sinα>0,cosα<0,且sin >cos
>cos ,则
,则 的取值范围是
的取值范围是
- A.(2kπ+
 ,2kπ+
,2kπ+ ),k∈Z
),k∈Z - B.(
 +
+ ,
, +
+ ),k∈Z
),k∈Z - C.(2kπ+
 ,2kπ+π),k∈Z
,2kπ+π),k∈Z - D.(2kπ+
 ,2kπ+
,2kπ+ )∪(2kπ+
)∪(2kπ+ ,2kπ+π),k∈Z
,2kπ+π),k∈Z
D
分析:先解sin >cos
>cos ,将
,将 看成整体,利用三角函数的性质得出
看成整体,利用三角函数的性质得出 +2kπ<
+2kπ< <
< +2kπ,k∈Z,结合不等式的性质得出
+2kπ,k∈Z,结合不等式的性质得出 +6kπ<α<
+6kπ<α< +6kπ,k∈Z①,又sinα>0,cosα<0,得到α是第二象限角②,由①②可进一步缩小角α的范围,从而得出答案.
+6kπ,k∈Z①,又sinα>0,cosα<0,得到α是第二象限角②,由①②可进一步缩小角α的范围,从而得出答案.
解答:∵sin >cos
>cos ,
,
∴ +2kπ<
+2kπ< <
< +2kπ,k∈Z,
+2kπ,k∈Z,
∴ +6kπ<α<
+6kπ<α< +6kπ,k∈Z,①
+6kπ,k∈Z,①
又sinα>0,cosα<0,
∴α是第二象限角,②
由①②可得: +6kπ<α<π+6kπ,或
+6kπ<α<π+6kπ,或 +6kπ<α<3π+6kπ,k∈Z,
+6kπ<α<3π+6kπ,k∈Z,
∴2kπ+ <
< <2kπ+
<2kπ+ 或2kπ+
或2kπ+ <
< <2kπ+π,k∈Z
<2kπ+π,k∈Z
故选D.
点评:本小题主要考查象限角、轴线角、三角不等式的解法、三角函数值的符号等基础知识,考查运算求解能力,考查转化思想.属于基础题.
分析:先解sin
 >cos
>cos ,将
,将 看成整体,利用三角函数的性质得出
看成整体,利用三角函数的性质得出 +2kπ<
+2kπ< <
< +2kπ,k∈Z,结合不等式的性质得出
+2kπ,k∈Z,结合不等式的性质得出 +6kπ<α<
+6kπ<α< +6kπ,k∈Z①,又sinα>0,cosα<0,得到α是第二象限角②,由①②可进一步缩小角α的范围,从而得出答案.
+6kπ,k∈Z①,又sinα>0,cosα<0,得到α是第二象限角②,由①②可进一步缩小角α的范围,从而得出答案.解答:∵sin
 >cos
>cos ,
,∴
 +2kπ<
+2kπ< <
< +2kπ,k∈Z,
+2kπ,k∈Z,∴
 +6kπ<α<
+6kπ<α< +6kπ,k∈Z,①
+6kπ,k∈Z,①又sinα>0,cosα<0,
∴α是第二象限角,②
由①②可得:
 +6kπ<α<π+6kπ,或
+6kπ<α<π+6kπ,或 +6kπ<α<3π+6kπ,k∈Z,
+6kπ<α<3π+6kπ,k∈Z,∴2kπ+
 <
< <2kπ+
<2kπ+ 或2kπ+
或2kπ+ <
< <2kπ+π,k∈Z
<2kπ+π,k∈Z故选D.
点评:本小题主要考查象限角、轴线角、三角不等式的解法、三角函数值的符号等基础知识,考查运算求解能力,考查转化思想.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤. 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E: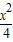
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E:
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E:
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.