题目内容
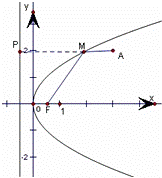
若点A的坐标为（3，2），F是抛物线y2=2x的焦点，点M在抛物线上移动时，使|MF|+|MA|取得最小值的M的坐标为 ．
解答： 解：由题意得 F（ 
，0），准线方程为 x=﹣，设点M到准线的距离为d=|PM|，
则由抛物线的定义得|MA|+|MF|=|MA|+|PM|，
故当P、A、M三点共线时，|MF|+|MA|取得最小值为|AP|=3﹣（﹣）=
．
把 y=2代入抛物线y2=2x 得 x=2，故点M的坐标是（2，2），
故答案为：（2，2）．
练习册系列答案
名校课堂系列答案
相关题目
若点A的坐标为（3，2），F是抛物线y2=2x的焦点，点M在抛物线上移动时，使|MF|+|MA|取得最小值的M的坐标为（ ）
| A、（0，0） | ||
B、(
| ||
C、(1，
| ||
| D、（2，2） |