题目内容
A=
，B={y|y=x2+x+1，x∈R}
（1）求A，B；
（2）求A∪B，A∩CRB．
解：（1）由
得，
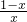≥0，即x（x-1）≤0且x≠0，解得0＜x≤1，
则A={x|0＜x≤1}，
由y=x2+x+1=
+
≥得，B={y|y≥}，
（2）由（1）得，如图：
∴A∪B={x|0＜x≤1}∪{y|y≥}=（0，+∞），
∵CRB={y|y＜}=（-∞，），∴A∩CRB=（0，）
分析：（1）把等价转化为x（x-1）≤0且x≠0，求出解集即为集合A，利用配方法求出二次函数y=x2+x+1的值域，即为集合B；
（2）借助于数轴和（1）的结果，求出A∪B和CRB，再求出A∩CRB．
点评：本题的考点是集合的交、并、补集运算，考查了解分式不等式和配方法求二次函数的值域，求交、并、补集时借助于数轴更直观．
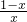得，≥0，即x（x-1）≤0且x≠0，解得0＜x≤1，则A={x|0＜x≤1}，
由y=x2+x+1=
+≥得，B={y|y≥}，（2）由（1）得，如图：
∴A∪B={x|0＜x≤1}∪{y|y≥
}=（0，+∞），∵CRB={y|y＜
}=（-∞，），∴A∩CRB=（0，）分析：（1）把
等价转化为x（x-1）≤0且x≠0，求出解集即为集合A，利用配方法求出二次函数y=x2+x+1的值域，即为集合B；（2）借助于数轴和（1）的结果，求出A∪B和CRB，再求出A∩CRB．
点评：本题的考点是集合的交、并、补集运算，考查了解分式不等式和配方法求二次函数的值域，求交、并、补集时借助于数轴更直观．
练习册系列答案
阅读快车系列答案
相关题目
已知a、b、m、n、x、y均为正数，且a≠b，若a、m、b、x成等差数列，a、n、b、y成等比数列，则有（ ）
| A、m＞n，x＞y | B、m＞n，x＜y | C、m＜n，x＜y | D、m＜n，x＞y |