题目内容
若函数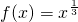
，则不等式f-1（x）＞f（x）的解集是________．
（-1，0）∪（1，+∞）
分析：先求出函数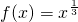的反函数f-1（x），然后代入不等式f-1（x）＞f（x），两边同取三次方，移项、因式分解可求出不等式的解集．
解答：∵
，x∈R
∴y3=x，x与y互换得y=x3；
∴f-1（x）=x3，
∵f-1（x）＞f（x）
∴x3＞
即x9＞x
∴x（x8-1）=x（x4-1）（x4+1）=x（x2-1）（x2+1）（x4+1）=x（x-1）（x+1）（x2+1）（x4+1）＞0
∴x∈（-1，0）∪（1，+∞）
故答案为：（-1，0）∪（1，+∞）
点评：本题主要考查了反函数，以及不等式的解法，解题的关键就是因式分解，属于基础题．
分析：先求出函数
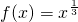的反函数f-1（x），然后代入不等式f-1（x）＞f（x），两边同取三次方，移项、因式分解可求出不等式的解集．解答：∵
，x∈R∴y3=x，x与y互换得y=x3；
∴f-1（x）=x3，
∵f-1（x）＞f（x）
∴x3＞
即x9＞x∴x（x8-1）=x（x4-1）（x4+1）=x（x2-1）（x2+1）（x4+1）=x（x-1）（x+1）（x2+1）（x4+1）＞0
∴x∈（-1，0）∪（1，+∞）
故答案为：（-1，0）∪（1，+∞）
点评：本题主要考查了反函数，以及不等式的解法，解题的关键就是因式分解，属于基础题．
练习册系列答案
天天练口算系列答案
相关题目
，则不等式f（x）＞g（x）的解集是（ ）
，则不等式f（a）＞f（1-a）的解集为
，则不等式f-1（x）＞f（x）的解集是 ．
，则不等式f（a）＞f（1-a）的解集为（ ）
