题目内容
设函数f(x)=(1+x)2-2ln(1+x)
(1)若关于x的不等式f(x)-m≥0在[0,e-1]有实数解,求实数m的取值范围;
(2)设g(x)=f(x)-x2-1,若关于x的方程g(x)=p至少有一个解,求p的最小值.
(3)证明不等式:ln(x+1)<1+![]() +
+![]() +…+
+…+![]() (n∈N*)
(n∈N*)
答案:
解析:
解析:
|
解:(1)依题意得 ∴ 即实数m的取值范围为 (2) 则 显然,函数 则函数 所以,要使方程 (3)由(2)可知: 所以 令 即 所以, 将以上n个等式相加即可得到: |

练习册系列答案
相关题目
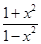 .
.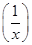 +f(x)=0.
+f(x)=0.