题目内容
已知函数f(x)=ax2-2x+1在(0,3]内有零点,则a的取值范围是
- A.

- B.[1,+∞)
- C.

- D.(-∞,1]
D
分析:先将f(x)=ax2-2x+1在(0,3]内有零点转化成方程ax2-2x+1=0在(0,3]内有解,然后将a分离出来,利用换元法求出等式另一侧的值域,从而求出a的取值范围.
解答:∵f(x)=ax2-2x+1在(0,3]内有零点
∴方程ax2-2x+1=0在(0,3]内有解
即a= =
= x∈(0,3]
x∈(0,3]
令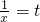 ∈[
∈[ ,+∞)
,+∞)
则a=2t-t2 t∈[ ,+∞)
,+∞)
∴a≤1
故选D.
点评:本题主要考查了函数零点的判定,以及参数分离法的应用和二次函数的值域,同时考查了转化的思想和换元法的运用,属于基础题.
分析:先将f(x)=ax2-2x+1在(0,3]内有零点转化成方程ax2-2x+1=0在(0,3]内有解,然后将a分离出来,利用换元法求出等式另一侧的值域,从而求出a的取值范围.
解答:∵f(x)=ax2-2x+1在(0,3]内有零点
∴方程ax2-2x+1=0在(0,3]内有解
即a=
 =
= x∈(0,3]
x∈(0,3]令
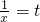 ∈[
∈[ ,+∞)
,+∞)则a=2t-t2 t∈[
 ,+∞)
,+∞)∴a≤1
故选D.
点评:本题主要考查了函数零点的判定,以及参数分离法的应用和二次函数的值域,同时考查了转化的思想和换元法的运用,属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目