Question

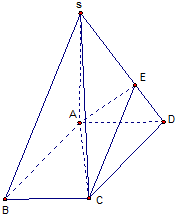（2012•陕西三模）如图，在四棱锥S-ABCD中，底面ABCD为平行四边形，SA⊥底面ABCD，AB=2，AD=1，SB=

7

，∠BAD=120°，E在棱SD上．
（Ⅰ）当SE为何值时，SB∥面ACE；
（Ⅱ）若SE=3ED时，求点D到面AEC的距离．

Answer 1

分析：（1）在平行四边形ABCD中，连接BD交AC于O，过O作OE∥SB交SD于E，则SB∥面ACE，O为BD的中点，所以E为SD的中点，然后求出SE．
（2）判断三角形ABC为直角三角形，求出AE，利用V_E-ADC=V_D-AEC，求出h为点D到面AEC的距离即可．

解答：解：（1）在平行四边形ABCD中，连接BD交AC于O，过O作OE∥SB交SD于E，则SB∥面ACE，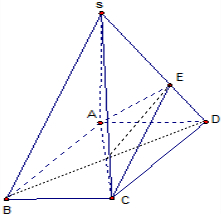
O为BD的中点，所以E为SD的中点，
SA⊥底面ABCD，AB=2，AD=1，SB=

7

，SA=

( 7 )2-22

=

3

，所以SD=

1+( 3 )2

=2，
E为SD的中点，所以SE=1，此时满足SB∥面ACE．
（2）因为AB=2，AD=1，∠BAD=120°，所以∠B=60°，三角形ABC为直角三角形，
AC⊥AD，因为SA⊥底面ABCD，所以AC⊥平面SAD，AE?平面SAD，
所以AC⊥AE，SE=3ED=

3

2

，ED=

1

2

，cos∠SDA=

AD

SD

=

1

2

，
AE=

AD2+DE2-2•AD•AEcos60°

=

3

2

，
因为V_E-ADC=V_D-AEC，
h为点D到面AEC的距离
所以

1

3

×

1

2

AD• AC•

SA

4

=

1

3

×

1

2

AC•AE•h，
即1• 

3

•

3

4

= 

3

•

3

2

•h，
计算得h=

1

2

，
点D到面AEC的距离为

1

2

．

点评：本题考查直线与平面平行，点到直线的距离的求法，等体积方法的应用，考查空间想象能力计算能力．