题目内容
如图,正方形
ABCD,有一直径为BC的半圆,BC=2cm,现有两点E、F,分别从点B、点A同时出发,点E沿线段BA以1cm/s的速度向点A运动,点F沿折线A-D-C以2 cm/s的速度向点C运动,设E离开点B的时间为t s.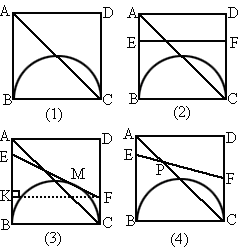
(1)
当t为何值时,线段EF与BC平行;(2)
设1<t<2,当t为何值时,EF与半圆相切?(3)
当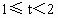 时,设EF与AC相交于点P,问点E、F运动时,点P的位置是否发生变化?若变化,请说明理由;若不变化,请给予证明,并求AP∶PC的值.
时,设EF与AC相交于点P,问点E、F运动时,点P的位置是否发生变化?若变化,请说明理由;若不变化,请给予证明,并求AP∶PC的值.
答案:略
解析:
提示:
解析:
|
解: (1)∵四边形ABCD为正方形,∴AB∥DC,而EF∥BC,∴BE=FC.∵BE=t,CF=4-2t,∴t=4-2t,得 ,即当 ,即当 时,线段EF∥BC. 时,线段EF∥BC.
(2) 设E、F出发t s时,EF与半圆相切,如图(3),∴EF=EM +MF=EB+FC(切线长定理).作 FK⊥AB,进而KB=FC.又 ∵ , ,
于是  , ,
即  ,解之,得 ,解之,得 . .
∵1 <t<2,∴ , ,
即当  时,EF与半圆相切. 时,EF与半圆相切.
(3) 当 时,点P的位置不会发生变化. 时,点P的位置不会发生变化.
事实上,设  时,E、F出发t s后的线段位置,如图(4), 时,E、F出发t s后的线段位置,如图(4),
则  , ,
而由 AB∥DC,有△APE∽△CPF,可知  ,这个比值显然与t无关,因而点P的位置不会发生变化. ,这个比值显然与t无关,因而点P的位置不会发生变化. |
提示:
|
分析:本题是典型的运动几何问题,用运动变化观点分析与看待此问题.对于(1)与(2)的解答均是先假设结论成立,逆向思考从而求出t的值.对于(3)讨论 |

练习册系列答案
相关题目
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= 8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:
8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论: 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE. (2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
(2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为