题目内容
定义“n次幂平均三角形”:如果△ABC的三边满足等式:b=(
)
(n∈Z),则称△ABC为“n次幂平均三角形”.如果△ABC为“2次幂平均三角形”,则角B的取值范围是( )
| an+cn |
| 2 |
| 1 |
| n |
A、(0,
| ||
B、(0,
| ||
C、(0,
| ||
D、(0,
|
分析:把b代入关于B的余弦定理中,化简整理后利用基本不等式求得cosB的范围,进而求得B的范围.
解答:解:由b=(
)
得,cosB=
=
=
=
≥
=
,
得到cosB≥
,0<B≤
.
故选C
| a2+c2 |
| 2 |
| 1 |
| 2 |
| a2+c2-b2 |
| 2ac |
a2+c2-(
| ||||
| 2ac |
a2+c2-
| ||
| 2ac |
| a2+c2 |
| 4ac |
| 2ac |
| 4ac |
| 1 |
| 2 |
得到cosB≥
| 1 |
| 2 |
| π |
| 3 |
故选C
点评:本题是三角函数的有关知识与不等式的综合.不等式作为一种工具,经常与其它知识综合考查.

练习册系列答案
相关题目

 (n∈Z),则称△ABC为“n次幂平均三角形”.如果△ABC为“2次幂平均三角形”,则角B的取值范围是
(n∈Z),则称△ABC为“n次幂平均三角形”.如果△ABC为“2次幂平均三角形”,则角B的取值范围是

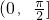
 (n∈Z),则称△ABC为“n次幂平均三角形”.如果△ABC为“2次幂平均三角形”,则角B的取值范围是( )
(n∈Z),则称△ABC为“n次幂平均三角形”.如果△ABC为“2次幂平均三角形”,则角B的取值范围是( )


