题目内容
已知曲线C:
(θ∈R),一动直线l过A(-1,0)与曲线C相交于P,Q两点,M为P,Q中点,l与直线x+3y+6=0相交于N,则|AM|•|AN|=
|
5
5
.分析:设连接CA并延长交直线x+3y+6=0相交于G,可得CG⊥NG,由垂径定理得CM⊥PQ,可得△AGN∽△AMC,将比例线段转化为等积式,得|AM|•|AN|=|AC|•|AG|=5.
解答:解:把曲线C:
(θ∈R) 消去参数θ化为普通方程为 x2+(y-3)2=4. 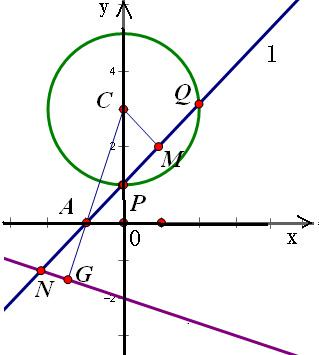
设连接CA并延长交直线x+3y+6=0相交于G,连接CM可得AC的斜率为kAC=
=3.
∵直线x+3y+6=0的斜率为K1=-
,kAC•k1=3×(-
)=-1,
∴直线AC与直线x+3y+6=0垂直.
又∵圆C中,M为弦PQ的中点,∴CM⊥PQ,
因此△AGN∽△AMC,可得
=
,∴|AM|•|AN|=|AC|•|AG|.
又∵|AC|=
=
,AG=
=
,
∴|AC|•|AG|=
×
=5,
故答案为 5.
|

设连接CA并延长交直线x+3y+6=0相交于G,连接CM可得AC的斜率为kAC=
| 3-0 |
| 0+1 |
∵直线x+3y+6=0的斜率为K1=-
| 1 |
| 3 |
| 1 |
| 3 |
∴直线AC与直线x+3y+6=0垂直.
又∵圆C中,M为弦PQ的中点,∴CM⊥PQ,
因此△AGN∽△AMC,可得
| AC |
| AN |
| AM |
| AG |
又∵|AC|=
| (-1-0)2+(3-0)2 |
| 10 |
| |-1+3×0+6| | ||
|
| ||
| 2 |
∴|AC|•|AG|=
| 10 |
| ||
| 2 |
故答案为 5.
点评:本题考查了直线与圆相交的性质,属于中档题,利用垂径定理得到三角形相似是解决本题的关键.

练习册系列答案
相关题目
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)