题目内容
(15分)数列{an},a1=1,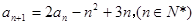
(1)求a2,a3的值;
(2)是否存在常数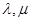 ,使得数列
,使得数列 是等比数列,若存在,求出
是等比数列,若存在,求出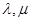 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)设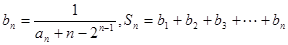 ,
,
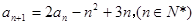
(1)求a2,a3的值;
(2)是否存在常数
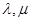 ,使得数列
,使得数列 是等比数列,若存在,求出
是等比数列,若存在,求出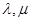 的值;若不存在,说明理由;
的值;若不存在,说明理由;(3)设
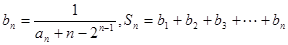 ,
,解:(1)

(2)设
 ,
,即

故

∴

又
 使得数列
使得数列  是等比数列
是等比数列(3)证明:由(1)得

∴
 ,故
,故
∵

∴

 ,现证
,现证
当n=2时,
 ,
,故n=2时不等式成立,当
 得
得
∵

略

练习册系列答案
相关题目
 为等差数列,
为等差数列, 为其前
为其前 项和,且
项和,且 ,则
,则 ( )
( ) 为等差数列
为等差数列 的前
的前 项的和,
项的和, ,
, ,则
,则 的值为
的值为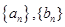 的前
的前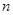 项和分别为
项和分别为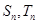 ,如果
,如果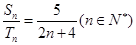 ,则
,则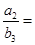 ____________.
____________.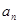 }中,
}中,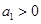 ,
,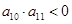 ,若此数列的前10项和
,若此数列的前10项和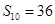 ,前18项和
,前18项和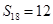 ,则数列{
,则数列{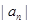 }的前18项和
}的前18项和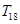 的值是
的值是 项的和
项的和 等于
等于



 是等差数列,
是等差数列, ,其前
,其前 项的和
项的和 ,其公差
,其公差 。
。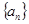 是单调递增的等差数列,
是单调递增的等差数列,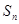 为其前n项和,且满足
为其前n项和,且满足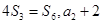 是
是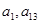 的等比中项.
的等比中项.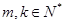 ,使
,使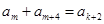 ?说明理由;
?说明理由;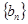 满足
满足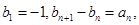 求数列
求数列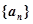 的前n项和为Sn,且
的前n项和为Sn,且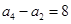 ,
,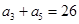 .记
.记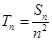 ,如果存在正整数M,使得对一切正整数n,
,如果存在正整数M,使得对一切正整数n,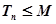
 都成立.则M的最小值是
都成立.则M的最小值是