Question

【题目】在中，，则____________.

Answer 1

【答案】

【解析】

根据余弦定理化简，得到；由题意，在BC上取D，使得BD＝AD，连接AD，找出A﹣B，设BD＝x，在△ADC中两次利用余弦定理将cos（A﹣B）及cosC表示出，分别求出x建立关于a，b的方程，化简变形后利用整体换元求出答案．

由题意知，4cosC，

∴由余弦定理得，4，

化简可得＝2，则,

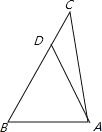
又中不妨设a＞b，∴A＞B．在BC上取D，使得BD＝AD，连接AD，

设BD＝x，则AD＝x，DC＝a﹣x，AC＝b，

在△ADC中， cos∠DAC＝cos（A﹣B），

由余弦定理得：（a﹣x）2＝x2+b2﹣2xb，

即：(b﹣6a)x＝，

解得：x＝．①

又在△ADC中，由余弦定理还可得cosC，

∴cosC，化简得x＝，②

由①②可得，又＝2，

联立可得=,即=,

两边同时除以，得=+6，令，则12，解得t=或，

又由题意，∴t=cosC=，

故答案为：.