题目内容
曲线y=e2x与直线x+y=1、x-1=0围成的平面图形的面积等于
- A.
e2-1 - B.e2-
- C.e2-
- D.e2-
A
分析：先求出曲线与直线的交点，设围成的平面图形面积为S，利用定积分求出S即可．
解答：由题意，曲线y=e2x与直线x+y=1、x-1=0围成的平面图形如图所示
∴S=
=（
）
=
-=
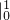
故选A．
点评：本题主要考查定积分求面积．用定积分求面积时，要注意明确被积函数和积分区间，属于基本运算．
分析：先求出曲线与直线的交点，设围成的平面图形面积为S，利用定积分求出S即可．
解答：由题意，曲线y=e2x与直线x+y=1、x-1=0围成的平面图形如图所示
∴S=
=（）=
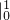
-=故选A．
点评：本题主要考查定积分求面积．用定积分求面积时，要注意明确被积函数和积分区间，属于基本运算．
练习册系列答案
相关题目
与函数y=e2x-2ex+1（x≥0）的曲线关于直线y=x对称的曲线的方程为（ ）
A、y=ln(1+
| ||
B、y=ln(1-
| ||
C、y=-ln(1+
| ||
D、y=-ln(1-
|
e2－1
e2－
e2－
e2-1
e2-
e2-
