题目内容
（理科）三个数a、b、c∈（0，
），且cosa=a，sin（cosb）=b，cos（sinc）=c，则a、b、c从小到大的顺序是______．
| π |
| 2 |
先证明当x∈（0，
）时，sinx＜x
设y=sinx-x，则y′=cosx-1＜0，∴y=sinx-x为（0，
）上的减函数，∴y＜sino-0=0，即sinx＜x
同理可证明f（x）=sin（cosx）-x为（0，
）上的减函数，g（x）=cos（sinx）-x为（0，
）上的减函数
∵sina＜a
∴cos（sina）-a=cos（sina）-cosa＞0，而cos（sinc）-c=0，
∴g（a）＞g（c），a、c∈（0，
），
∴a＜c
同理∵x∈（0，
）时，sinx＜x，∴sin（cosa）＜cosa
∴sin（cosa）-a=sin（cosa）-cosa＜0，而sin（cosb）-b=0
∴f（a）＜f（b），a、b∈（0，
），
∴a＞b
综上所述，b＜a＜c
故答案为b＜a＜c
| π |
| 2 |
设y=sinx-x，则y′=cosx-1＜0，∴y=sinx-x为（0，
| π |
| 2 |
同理可证明f（x）=sin（cosx）-x为（0，
| π |
| 2 |
| π |
| 2 |
∵sina＜a
∴cos（sina）-a=cos（sina）-cosa＞0，而cos（sinc）-c=0，
∴g（a）＞g（c），a、c∈（0，
| π |
| 2 |
∴a＜c
同理∵x∈（0，
| π |
| 2 |
∴sin（cosa）-a=sin（cosa）-cosa＜0，而sin（cosb）-b=0
∴f（a）＜f（b），a、b∈（0，
| π |
| 2 |
∴a＞b
综上所述，b＜a＜c
故答案为b＜a＜c
练习册系列答案
相关题目
，
，
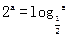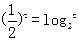，则a、b、c从小到大的顺序是_________________.
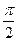)，且cosa=a，sin(cosb)=b，cos(sinc)=c，则a、b、c从小到大的顺序是_____________
，
，
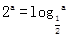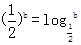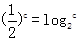，则a、b、c从小到大的顺序是_________________.
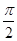)，且cosa=a，sin(cosb)=b，cos(sinc)=c，则a、b、c从小到大的顺序是_____________
），且cosa=a，sin（cosb）=b，cos（sinc）=c，则a、b、c从小到大的顺序是________．