题目内容
已知函数f(x)=sin(2x+ )+sin(2x-
)+sin(2x- )-cos2x
)-cos2x
(Ⅰ)求函数f(x)的最小正周期和单调增区间;
(Ⅱ)若函数f(x)的图像向左平移 m(m>0)个单位后,得到函数g(x)的图像关于y轴对称,求实数m的最小值.
解:(Ⅰ)f(x)=sin(2x+ )+sin(2x-
)+sin(2x- )-cos2x
)-cos2x
= sin2x-cos2x=2sin(2x-
sin2x-cos2x=2sin(2x- ),--
),--
∴f(x)的最小正周期为 =π. -
=π. -
当2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ (k∈Z),
(k∈Z),
即kπ- ≤x≤kπ+
≤x≤kπ+ (k∈Z)时,函数f(x)单调递增,
(k∈Z)时,函数f(x)单调递增,
故所求区间为[kπ- ,kπ+
,kπ+ ](k∈Z).-
](k∈Z).-
(Ⅱ)函数f(x)的图像向左平移m(m>0)个单位后得g(x)=2sin[2(x+m)- ],
],
要使g(x)的图像关于y轴对称,
只需2m- =kπ+
=kπ+ (k∈Z).
(k∈Z).
即m= +
+ (k∈Z).所以m的最小值为
(k∈Z).所以m的最小值为 .-
.-

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 不等式
不等式 的解集是R,命题
的解集是R,命题 在区间
在区间 上是减函数,若命题“
上是减函数,若命题“ ”为真,则实数
”为真,则实数 的范围是____.
的范围是____.
 的焦点为圆心,且与双曲线
的焦点为圆心,且与双曲线 的渐近线相切的圆的方程为( )
的渐近线相切的圆的方程为( ) (B)
(B)
 (D)
(D)
 (-2,-1)在直线
(-2,-1)在直线 上,其中
上,其中 ,则
,则 的最小值为 .
的最小值为 . 的值是( )
的值是( )  D.
D. 
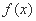 对任意
对任意 都有
都有 的图象关于点
的图象关于点 对称,则
对称,则 ( )
( ) C.5 D.0
C.5 D.0 满足
满足 ,则
,则 .
. ,使
,使 >3”的否定是“
>3”的否定是“ ,使
,使 3”;
3”; 的最小正周期是
的最小正周期是 ;
; 中,若
中,若 ,则
,则 ”的逆命题是真命题;
”的逆命题是真命题; ”是“直线
”是“直线 和直线
和直线 垂直”的充要条件;其中正确的说法是 (只填序号).
垂直”的充要条件;其中正确的说法是 (只填序号).