题目内容
设数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意的
,且对任意的![]() ,都有
,都有![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求数列![]() 的通项公式
的通项公式![]() ;
;
(3)证明:![]() .
.
(1)![]()
![]() (2)
(2)![]() (3)见解析
(3)见解析
解析:
(1)解:当![]() 时,有
时,有![]() ,
,
由于![]() ,所以
,所以![]() .
.
当![]() 时,有
时,有![]() ,即
,即![]() ,
,
将![]() 代入上式,由于
代入上式,由于![]() ,所以
,所以![]() .
.
(2)解:由![]() ,
,
得![]() , ①
, ①
则有![]() . ②
. ②
②-①,得![]() ,
,
由于![]() ,所以
,所以![]() . ③
. ③
同样有![]()
![]() , ④
, ④
③-④,得![]() .
.
所以![]() .
.
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
由于![]() ,即当
,即当![]() 时都有
时都有![]() ,所以数列
,所以数列![]() 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
故![]() .
.
(3)证明1:由于![]() ,
,
![]() ,
,
所以![]() .
.
即![]() .
.
令![]() ,则有
,则有![]() .
.
即![]() ,
,
即![]()
故![]() .
.
证明2:要证![]() ,
,
只需证![]() ,
,
只需证![]() ,
,
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
只需证![]() .
.
由于![]()
![]()
![]()
![]() .
.
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
因此原不等式成立.

 的前
的前 项和为
项和为 ,且
,且 .
. ,数列
,数列 的前
的前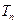 ,求证:
,求证: .
. 的前
的前 项和为
项和为 ,且满足
,且满足 .
. 与
与 两项之间插入
两项之间插入 个数构成等差数列,其公差为
个数构成等差数列,其公差为 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且满足
,且满足
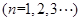 .
. 为等比数列;
为等比数列; ;
; 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列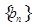 的前
的前 .
. 
 的前
的前 项和为
项和为 ,且
,且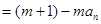 对于
对于 为常数,且
为常数,且
 ,数列
,数列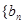

 ,
,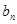
 )(
)( ,
, ,求证:数列
,求证:数列

