Question

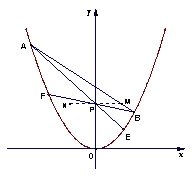
（江西卷文22）已知抛物线和三个点

，过点的一条直线交抛物线于、两点，的延长线分别交曲线于．

（1）证明三点共线；

（2）如果、、、四点共线，问：是否存在，使以线段为直径的圆与抛物线有异于、的交点？如果存在，求出的取值范围，并求出该交点到直线的距离；若不存在，请说明理由．

Answer 1

（1）证明：设，

则直线的方程：       

即：

因在上，所以①   

又直线方程：

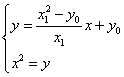由得：

所以     

同理，

所以直线的方程：   

令得

将①代入上式得，即点在直线上，所以三点共线                           

（2）解：由已知共线，所以 

以为直径的圆的方程：

由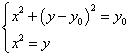得

所以（舍去），        

要使圆与抛物线有异于的交点，则

所以存在，使以为直径的圆与抛物线有异于的交点 

则，所以交点到的距离为