Question

已知等差数列{a_n}中，a₁₅=33,a₆₁=217,试判断153是不是这个数列的项，如果是，是第几项？

Answer 1

思路分析：可由已知得到关于a₁,d的方程组，可求得通项公式a_n,于是判断153是否是这个数列的项的问题就转化为关于n的方程a_n=153是否有自然数解的问题.

解法一：设等差数列{a_n}的首项为a₁,公差为d,则a_n=a₁+(n-1)d.

由已知，得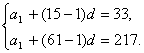

∴a₁=-23,d=4.

∴a_n=-23+(n-1)×4=4n-27.

令a_n=153,即4n-27=153,∴n=45,45∈N₊.

∴153是所给数列的第45项.

解法二：由等差数列性质得a₆₁-a₁₅=46d=217-33=184.

∴d=4.

又a_n=a₁₅+(n-15)d,∴153=33+4(n-15).

得n=45.

解法三：由等差数列的几何意义，其图象为一些共线的点，由于P（15，33），Q（n,153),R(61,217)共线，故，解得n=45.