题目内容
10.已知球的直径为20,当它的内接正四棱锥体积最大时,该四棱锥的高为$\frac{40}{3}$.分析 先设正四棱锥S-ABCD的底面边长等于a,底面到球心的距离等于x,得到x与a,R之间的关系,又正四棱锥的高为h=R+x,从而得出正四棱锥体积关于x函数表达式,最后利用基本不等式求出这个正四棱锥体积的最大值即可
解答 解:设正四棱锥S-ABCD的底面边长等于a,底面到球心的距离等于x
则:x2+($\frac{\sqrt{2}}{2}$a)2=100
而正四棱锥的高为h=10+x
故正四棱锥体积为:
V(x)=$\frac{1}{3}$a2h=$\frac{1}{3}$(200-2x2)(10+x)=$\frac{2}{3}$(100-x2)(10+x)=$\frac{1}{3}$(20-2x)(10+x)(10+x)
≤$\frac{1}{3}$×($\frac{20-2x+10+x+10+x}{3}$)3=$\frac{64000}{81}$
当且仅当x=$\frac{10}{3}$时,等号成立
那么正四棱锥的高为h=$\frac{40}{3}$.
故答案为:$\frac{40}{3}$.
点评 本题主要考查了球内接多面体、棱柱、棱锥、棱台的体积等基本知识,考查了空间想象力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.设复数z1=-1+i,z2=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,则$\frac{{z}_{1}}{{z}_{2}}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.某几何体的三视图如图所示,它的表面积为( )
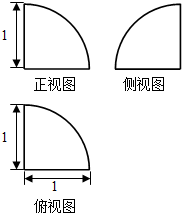

| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{7π}{8}$ | D. | π |
10.定义运算“•”如下:x•y=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若函数f(x)=m-(1-2x)•(2x-2)有两个零点,则( )
| A. | m∈(-$\frac{1}{2}$,+∞) | B. | m∈(-$\frac{1}{2}$,1) | C. | m∈[-$\frac{1}{2}$,+∞) | D. | m∈[-$\frac{1}{2}$,1) |
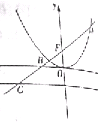 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.