题目内容
如图,在棱长为2的正方体ABCD—A1B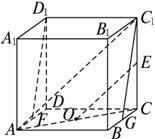
A.
B.
C.
D.
解析:如图,取BC中点G,连结GC1,则GC1∥FD1,连结AC1、AC,则OE∥AC1, ∴∠AC 由余弦定理得cosAC 故选B. 答案:B
.
练习册系列答案
考点解析与知能训练系列答案
阶梯听力系列答案
英语听读空间系列答案
英语听力教程系列答案
英语同步练习册系列答案
青苹果同步评价手册系列答案
初中英语知识集锦系列答案
小学语文词语手册吉林教育出版社系列答案
初中总复习中考精编系列答案
创新金卷毕业升学系列答案
相关题目
如图，在棱长为2的正四面体A-BCD中，若以△ABC为视角正面，则其正视图的面积是（ ）
