题目内容
如图，四面体ABCD中，E，G分别为BC，AB的中点，F在CD上，H在AD上，且有DF：FC=2：3。DH：HA=2：3。求证：EF，GH，BD交于一点。
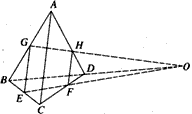
解：连接GE，HF，
∵E，G分别为BC，AB的中点，
∴GE∥AC
又∵DF：FC=2：3，DH：HA=2：3，
∴HF∥AC
∴GE∥HF
故G，E，F ，H四点共面
又∵EF与GH不能平行，
∴EF与GH相交，设交点为O
则O∈面ABD，O∈面BCD，而平面ABD∩平面BCD=BD
∴EF ，GH，BD交于一点。
∵E，G分别为BC，AB的中点，
∴GE∥AC
又∵DF：FC=2：3，DH：HA=2：3，
∴HF∥AC
∴GE∥HF
故G，E，F ，H四点共面
又∵EF与GH不能平行，
∴EF与GH相交，设交点为O
则O∈面ABD，O∈面BCD，而平面ABD∩平面BCD=BD
∴EF ，GH，BD交于一点。
练习册系列答案
相关题目
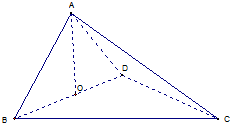如图，四面体ABCD中，O是BD的中点，△ABD和△BCD均为等边三角形，
如图，四面体ABCD中，0是BD的中点，CA=CB=CD=BD=a，AB=AD=
如图，四面体ABCD的各个面都是直角三角形，已知AB⊥BC，BC⊥CD，AB=a，BC=a，CD=c．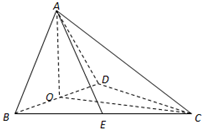
如图，四面体ABCD中，O、E分别是BD、BC的中点，AO⊥平面BCD，CA=CB=CD=BD=2．