题目内容
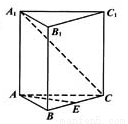
(本小题满分12分)如图,已知正三棱柱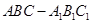 的各棱长都是4,
的各棱长都是4, 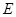 是
是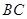 的中点,动点
的中点,动点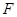 在侧棱
在侧棱 上,且不与点
上,且不与点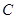 重合.
重合.
(I)当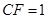 时,求证:
时,求证: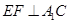 ;
;
(II)设二面角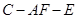 的大小为
的大小为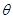 ,求
,求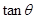 的最小值.
的最小值.
【答案】
解法一:过E作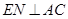 于N,连结EF.
于N,连结EF.
(I)如图1,连结NF、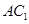 ,由直棱柱的性质知,底面ABC
,由直棱柱的性质知,底面ABC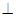 侧面
侧面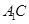 .
.
又底面 侧面
侧面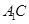 =AC,且
=AC,且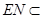 底面ABC,所以
底面ABC,所以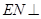 侧面
侧面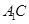 ,
,
∴NF为EF在侧面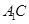 内的射影,
内的射影,
在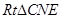 中,
中, =1,则由
=1,则由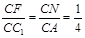 ,得NF//
,得NF//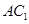 ,
,
又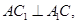 故
故 ,由三垂线定理知
,由三垂线定理知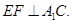
(II)如图2,连结AF,过N作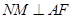 于M,连结ME,由(I)知
于M,连结ME,由(I)知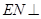 侧面
侧面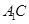 ,
,
根据三垂线定理得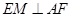 ,所以
,所以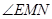 是二面角C—AF—E的平面角,即
是二面角C—AF—E的平面角,即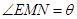 .
.
设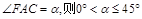 ,在
,在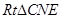 中,
中,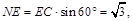
在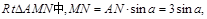 故
故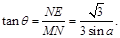
又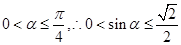 ,故当
,故当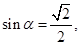 即当
即当 时,
时,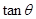 达到最小值,
达到最小值,
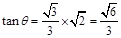 ,此时F与
,此时F与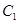 重合.
重合.
解法二:(I)建立如图3所示的空间直角坐标系,则由已知可得
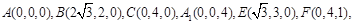
于是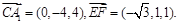

故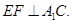
(II)设 平面AEF的一个法向量为
平面AEF的一个法向量为 ,
,
则由(I)得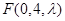 ,
,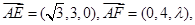
于是由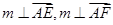 可得
可得

取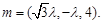
又由直三棱柱的性质可取侧面
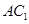 的一个法向量为
的一个法向量为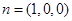 ,
,
于是由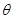 为锐角可得
为锐角可得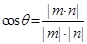
 ,∴
,∴ ,
,
由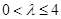 ,得
,得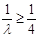 ,即
,即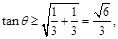
故当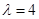 ,即点F与点
,即点F与点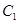 重合时,
重合时,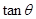 取得最小值
取得最小值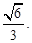
【解析】略

练习册系列答案
相关题目