题目内容
设函数f(x)=2x2+mx+n,求证:|f(1)|,|f(2)|,|f(3)|中至少有一个不小于1.
解:假设原命题不成立,
即|f(1)|,|f(2)|,|f(3)|都小于1.
则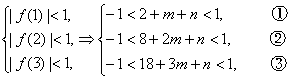
①+③得-11<2m+n<-9与②矛盾,所以假设不成立,即|f(1)|,|f(2)|,|f(3)|中至少有一个不小于1.

练习册系列答案
相关题目
题目内容
设函数f(x)=2x2+mx+n,求证:|f(1)|,|f(2)|,|f(3)|中至少有一个不小于1.
解:假设原命题不成立,
即|f(1)|,|f(2)|,|f(3)|都小于1.
则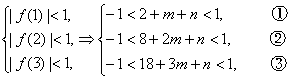
①+③得-11<2m+n<-9与②矛盾,所以假设不成立,即|f(1)|,|f(2)|,|f(3)|中至少有一个不小于1.
