题目内容

8．讨论函数f（x）=loga（3x2-2x-1）的单调性．

分析 先求出函数的定义域，进而结合二次函数的图象和性质，对数函数的图象和性质，复合函数单调性“同增异减”的原则，可得函数的单调性．

解答 解：由3x2-2x-1＞0得：x∈（-∞，-$\frac{1}{3}$）∪（1，+∞），
令t=3x2-2x-1，则t=3x2-2x-1在（-∞，-$\frac{1}{3}$）上为减函数，在（1，+∞）上为增函数，
当0＜a＜1时，y=logat为减函数，
故函数f（x）=loga（3x2-2x-1）在（-∞，-$\frac{1}{3}$）上为增函数，在（1，+∞）上为减函数，
当a＞11时，y=logat为增函数，
故函数f（x）=loga（3x2-2x-1）在（-∞，-$\frac{1}{3}$）上为减函数，在（1，+∞）上为增函数．

点评 本题考查的知识点是二次函数的图象和性质，对数函数的图象和性质，复合函数的单调性，难度中档．

练习册系列答案
相关题目
14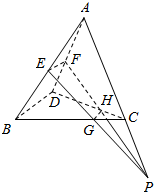．已知空间四边形ABCD中，E，F分别是AB，AD的中点，G，H分别是BC，CD上的点，且$\frac{BG}{GC}=\frac{DH}{HC}$=2，求证：直线EG，FH，AC相交于同一点P．
19．已知函数f（x）=$\frac{{a{x^2}}}{b+cx}$（a，b，c为常数），a，b分别是双曲线x2-$\frac{y^2}{3}$=1的实半轴长、半焦距，且直线x-cy=2和直线y=x-3垂直．
（1）求函数f（x）的解析式；
（2）设k＞1，解关于x的不等式f（x）＜$\frac{{（{k+1}）x-k}}{2-x}$．
16．定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界．已知函数$f（x）={（\frac{1}{4}）^x}+a•{（\frac{1}{2}）^x}-1$，g（x）=$\frac{1-m•{2}^{x}}{1+m•{2}^{x}}$．
（Ⅰ）当a=1时，求函数f（x）在（-∞，0）上的值域，并判断函数f（x）在（-∞，0）上是否为有界函数，请说明理由；
（Ⅱ）当m=1时，判断函数g（x）的奇偶性并证明，并判断g（x）是否有上界，并说明理由；
（Ⅱ）若函数f（x）在[0，+∞）上是以2为上界的有界函数，求实数a的取值范围；
（ IV）若m＞0，函数g（x）在[0，1]上的上界是G，求G的取值范围．
3．已知函数f（x）=x3-x．
（Ⅰ）求f（x）在区间[-2，0]上的最大值；
（Ⅱ）若过点P（2，t）存在3条直线与曲线y=f（x）相切，求t的取值范围．
13．若关于x的方程lg3x×lg4x-a2=0有两个不相等的实数根，则方程的两根之积为$\frac{1}{12}$．
20．若函数$f（x）={3^{{x^2}-2ax+5}}$在区间（-∞，1]内单调递减，则a的取值范围是（　　）
A．[1，+∞）B．（1，+∞）C．[1，3）D．[1，3]
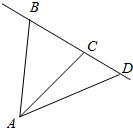17．如图，设A，B，C是不共线的三点，$\overrightarrow{AB}=\overrightarrow p，\overrightarrow{AC}=\overrightarrow q$，若点D在线段BC上，且BC：CD=5：2，则向量$\overrightarrow{AD}$=$\frac{7}{5}\overrightarrow{q}-\frac{2}{5}\overrightarrow{p}$（用向量$\overrightarrow p，\overrightarrow q$表示）．
18．二个数390，455的最大公约数是（　　）
A．64B．65C．66D．68

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网