题目内容
若A,B,C是平面直角坐标系中的共线三点,且  ,
,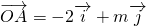 ,
,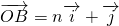 ,
,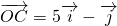 ,(其中
,(其中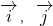 分别是直角坐标系x轴,y轴方向上的单位向量,O为坐标原点),求实数m,n的值.
分别是直角坐标系x轴,y轴方向上的单位向量,O为坐标原点),求实数m,n的值.
解:∵ ,
,
∴-2n+m=0,①…(2分)
∵A、B、C三点在同一直线上,
∴存在唯一的实数λ使得 ,…(6分)
,…(6分)
而 ,
, ,…(8分)
,…(8分)
∴ ,
,
消去λ得到mn-5m+n+9=0. ②…(10分)
由①得到m=2n,代入②解得:m=6,n=3或 . …(13分)
. …(13分)
分析:由已知中且 ,
,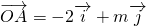 ,
,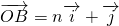 ,我们由向量垂直的充要条件可以得到
,我们由向量垂直的充要条件可以得到 =0,进而得到-2n+m=0,由A,B,C是平面直角坐标系中的共线三点,结合向量共线的充要条件,可以得到mn-5m+n+9=0,联立方程,即可求出实数m,n的值.
=0,进而得到-2n+m=0,由A,B,C是平面直角坐标系中的共线三点,结合向量共线的充要条件,可以得到mn-5m+n+9=0,联立方程,即可求出实数m,n的值.
点评:本题考查的知识点是平面向量的基本定理及其意义,平行向量与共线向量,熟练掌握向量垂直及平行(共线)的充要条件,是解答本题的关键.
 ,
,∴-2n+m=0,①…(2分)
∵A、B、C三点在同一直线上,
∴存在唯一的实数λ使得
 ,…(6分)
,…(6分)而
 ,
, ,…(8分)
,…(8分)∴
 ,
,消去λ得到mn-5m+n+9=0. ②…(10分)
由①得到m=2n,代入②解得:m=6,n=3或
 . …(13分)
. …(13分)分析:由已知中且
 ,
,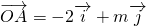 ,
,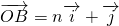 ,我们由向量垂直的充要条件可以得到
,我们由向量垂直的充要条件可以得到 =0,进而得到-2n+m=0,由A,B,C是平面直角坐标系中的共线三点,结合向量共线的充要条件,可以得到mn-5m+n+9=0,联立方程,即可求出实数m,n的值.
=0,进而得到-2n+m=0,由A,B,C是平面直角坐标系中的共线三点,结合向量共线的充要条件,可以得到mn-5m+n+9=0,联立方程,即可求出实数m,n的值.点评:本题考查的知识点是平面向量的基本定理及其意义,平行向量与共线向量,熟练掌握向量垂直及平行(共线)的充要条件,是解答本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点. ,定义f(P)=(m,n,p),其中m、n、p分别表示△MBC、△MCA、△MAB的面积,若
,定义f(P)=(m,n,p),其中m、n、p分别表示△MBC、△MCA、△MAB的面积,若 ,则在平面直坐标系中点(x,y)的轨迹是( )
,则在平面直坐标系中点(x,y)的轨迹是( )


